问题描述

有 $N$ 个球和 $N+1$ 个线性排列的孔。球从左到右依次编号为 $1$ 到 $N$，孔从左到右依次编号为 $1$ 到 $N+1$。第 $i$ 个球位于第 $i$ 个孔和第 $(i+1)$ 个孔之间。我们用 $d_i$ ($1 \leq i \leq 2 \times N$) 表示相邻物体（一个球和一个孔）从左到右的距离。给定两个参数 $d_1$ 和 $x$，对于所有 $i$ ($2 \leq i \leq 2 \times N$)，$d_i - d_{i-1}$ 都等于 $x$。

我们想要逐个将所有 $N$ 个球推入孔中。当一个球滚过一个孔时，如果这个孔里还没有球，那么球将掉入该孔中。否则，球将继续滚动并经过该孔。（在这个问题考虑的任何情况下，球不会碰撞。）

每一步，我们将均匀随机地选择剩余的球之一，然后均匀随机地选择一个方向（左或右），并将球推向该方向。请计算在此过程中所有球滚动的期望总距离。

例如，当 $N = 3$，$d_1 = 1$ 和 $x = 1$ 时，以下是一种可能的情况：

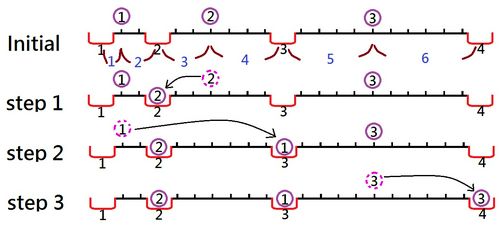
• 第一步：将编号为 $2$ 的球向左推动，它将掉入编号为 $2$ 的孔。滚动的距离为 $3$。
• 第二步：将编号为 $1$ 的球向右推动，它将经过编号为 $2$ 的孔并掉入编号为 $3$ 的孔。滚动的距离为 $9$。
• 第三步：将编号为 $3$ 的球向右推动，它将掉入编号为 $4$ 的孔。滚动的距离为 $6$。

所以这种情况下的总距离为 $18$。

请注意，在所有情况下，每个球都会掉入某个孔中，并且最后会有一个不含球的孔。

约束条件

• $1 \leq N \leq 200,000$
• $1 \leq d_1 \leq 100$
• $0 \leq x \leq 100$
• 所有输入值均为整数。

输入

从标准输入读取输入数据，格式如下：

$N$ $d_1$ $x$

输出

打印一个浮点数，表示答案。您的答案的相对误差或绝对误差不应大于 $10^{-9}$。

样例输入 1

1 3 3

样例输出 1

4.500000000000000

唯一球与左孔之间的距离为 $3$，与右孔之间的距离为 $6$。只有两种情况（即向左推和向右推）。唯一的球分别滚动了距离 $3$ 和 $6$，所以此示例的答案是 $(3+6)/2 = 4.5$。

样例输入 2

2 1 0

样例输出 2

2.500000000000000

样例输入 3

1000 100 100

样例输出 3

649620280.957660079002380