题目描述

给定一个不包含自环和重复边的 $N$ 个顶点、$M$ 条边的无向连通图。
第 $i$ 条边 $(1 \leq i \leq M)$ 连接顶点 $a_i$ 和顶点 $b_i$。

如果移除某条边后图变为不连通，则称该边为 桥。
请计算在这 $M$ 条边中有多少条是桥。

注意事项

• 自环指的是 $a_i=b_i$ 的边 $(1 \leq i \leq M)$。
• 重复边指的是一对边 $i,j$，满足 $a_i=a_j$ 且 $b_i=b_j$ $(1 \leq i<j \leq M)$。
• 当任意两个顶点之间存在路径时，该无向图被称为连通图。

约束条件

• $2 \leq N \leq 50$
• $N-1 \leq M \leq \min(N(N−1)⁄2,50)$
• $1 \leq a_i<b_i \leq N$
• 给定的图不包含自环和重复边。
• 给定的图是连通图。

输入

输入通过标准输入给出，格式如下：

$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$ $:$
$a_M$ $b_M$

输出

打印在这 $M$ 条边中有多少条是桥。

示例输入 1

7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7

示例输出 1

4

下图显示了给定的图：

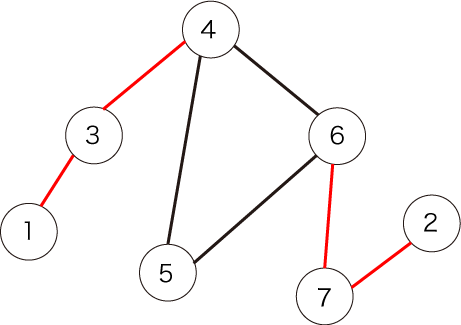
红色标记的边是桥，总共有四条。

示例输入 2

3 3
1 2
1 3
2 3

示例输出 2

0

可能不存在桥。

示例输入 3

6 5
1 2
2 3
3 4
4 5
5 6

示例输出 3

5

每一条边都可能是桥。