#abc075c. [abc075_c]Bridge
[abc075_c]Bridge
Problem Statement
You are given an undirected connected graph with vertices and edges that does not contain self-loops and double edges.
The -th edge connects Vertex and Vertex .
An edge whose removal disconnects the graph is called a bridge.
Find the number of the edges that are bridges among the edges.
Notes
- A self-loop is an edge such that .
- Double edges are a pair of edges such that and .
- An undirected graph is said to be connected when there exists a path between every pair of vertices.
Constraints
- The given graph does not contain self-loops and double edges.
- The given graph is connected.
Input
Input is given from Standard Input in the following format:
Output
Print the number of the edges that are bridges among the edges.
Sample Input 1
7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7
Sample Output 1
4
The figure below shows the given graph:
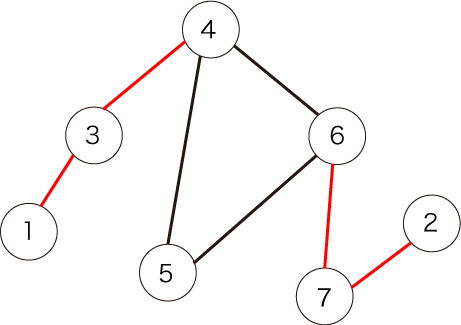
The edges shown in red are bridges. There are four of them.
Sample Input 2
3 3
1 2
1 3
2 3
Sample Output 2
0
It is possible that there is no bridge.
Sample Input 3
6 5
1 2
2 3
3 4
4 5
5 6
Sample Output 3
5
It is possible that every edge is a bridge.
