問題文

自己ループと二重辺を含まない $N$ 頂点 $M$ 辺の無向連結グラフが与えられます。
$i(1≦i≦M)$ 番目の辺は頂点 $a_i$ と頂点 $b_i$ を結びます。

グラフから辺を取り除いたとき、グラフ全体が非連結になるような辺のことを橋と呼びます。
与えられた $M$ 本のうち橋である辺の本数を求めてください。

ノート

• 自己ループ とは、$a_i=b_i(1≦i≦M)$ であるような辺 $i$ のことをいいます。
• 二重辺 とは、$a_i=a_j$ かつ $b_i=b_j(1≦i<j≦M)$ であるような辺の組 $i,j$ のことをいいます。
• 無向グラフが 連結 であるとは、グラフの任意の二頂点間に経路が存在することをいいます。

制約

• $2≦N≦50$
• $N-1≦M≦min(N(N−1)⁄2,50)$
• $1≦a_i<b_i≦N$
• 与えられるグラフは自己ループと二重辺を含まない。
• 与えられるグラフは連結である。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$
$a_1$ $b_1$
$a_2$ $b_2$ $:$
$a_M$ $b_M$

出力

$M$ 本の辺のうち、橋である辺の本数を出力せよ。

入力例 1

7 7
1 3
2 7
3 4
4 5
4 6
5 6
6 7

出力例 1

4

与えられるグラフは以下の図で表されます。

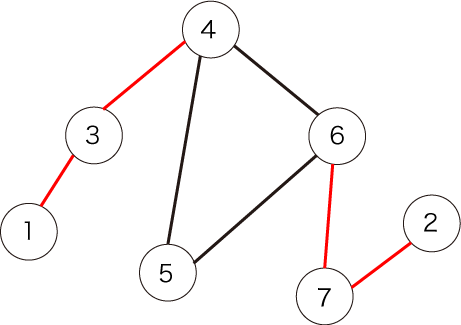
図の赤い辺が橋であり、その数は $4$ 本です。

入力例 2

3 3
1 2
1 3
2 3

出力例 2

0

橋である辺が存在しない場合もあります。

入力例 3

6 5
1 2
2 3
3 4
4 5
5 6

出力例 3

5

全ての辺が橋である場合もあります。