题目描述

睁开眼睛，A君发现自己在一个漆黑的房间里，他身处在一个由 $N$ 个房间(其中 $M$ 间是小黑屋)组成的迷宫内，但是不知道自己在哪个房间，现在你有这个迷宫的地图，你需要带领A君走出迷宫。

虽然A君不知道自己在哪，但是他面前有 $K$ 条道路，你可以通过许多指令告诉他该走第几条道路最终到达明亮的屋子。当然，如果指令还未结束，但A君已经到达明亮的屋子时，他便不会再执行指令。

注意：你不知道A君在哪个小黑屋，所以你需要给A君一串万能的指令，让他无论在哪个小黑屋，都可以通过这串指令走到明亮的屋子。

由于A君的记忆力不好，所以你需要让这串指令的长度尽可能的小，问这串指令的最短长度。

输入格式

第一行三个整数 $N,M,K$。

第二行 $M$ 个整数，$D_i$ 代表第 $i$ 个小黑屋编号是 $D_i$。

接下来 $N$ 行，每行 $K$ 个整数 $v_{i,j}$，第 $i$ 行第 $j$ 个数表示房间 $i$ 到房间 $j$ 有一条单向道路（可能存在自环）。

输出格式

一个整数，代表最短的指令长度。

说明/提示

数据规模与约定

$2\ \leq\ N\ \leq\ 100$，

$1\ \leq\ M\ \leq\ min(16,\ N-1)$，

$1\ \leq\ K\ \leq\ N$，

$1\ \leq\ D_i\ \leq\ N$，

$1\ \leq\ v_{i,\ j}\ \leq\ N$

保证每个 $D_i$ 不相同，且每个小黑屋都至少有一条路径可以到达明亮的屋子。

样例解释1

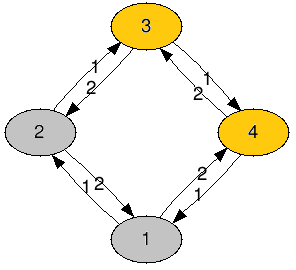
如果你给出指令 1,1，

当A君在 $1$ 号屋子时，他会走道路 $v_{1,1}$（即道路 $1$） 到达 $2$ 号屋子，再从 $2$ 号屋子走 $v_{2,1}$ 到达 $3$ 号屋子（亮屋）。

当A君在 $2$ 号屋子时，他会走 $v_{2,1}$ 到达 $3$ 号屋子，由于此时A君已经到达明亮的屋子，所以他不会再去执行下一条指令（即从 $3$ 号屋子走 $v_{3,1}$ 到达 $4$ 号屋子）。

样例解释2

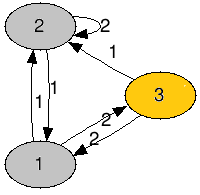
如果你给出指令 2,1,2，

当A君在 $1$ 号屋子时，他会走 $v_{1,2}$ 到达 $3$ 号屋子（此时情况处理见样例解释1）。

当A君在 $2$ 号屋子时，他会走 $v_{2,2}$ 到达 $2$ 号屋子，走 $v_{2,1}$ 到达 $1$ 号屋子，走 $v_{1,2}$ 到达 $3$ 号屋子。

样例解释3

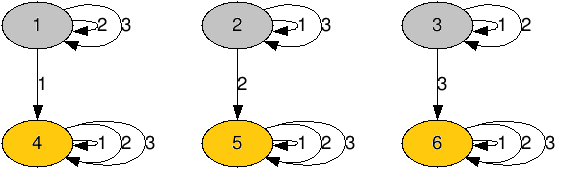
此时给出指令 1,2,3 即可。

注意

要求输出指令的最短长度，而不是指令。