問題文

二次元平面上で， $(x_i,y_i)$ からのマンハッタン距離が ちょうど $r_i$ であるような点の集合から成る図形が $n$ 個ある． どの $2$ つの図形についても，それらを構成する点集合同士は共通部分を持たない．

このとき，「座標 $(x1,y1)$ から座標 $(x2,y2)$ に移動するときに通過しなければならない最小の点の数を答えよ」というクエリが $m$ 個与えられるので順番に答えよ． クエリで与えられる $2$ つの座標は，どの図形の点集合にも含まれないことが保障されている．

移動の際，任意の実数座標を移動することが出来るとして良い．

入力

入力は以下の形式で標準入力から与えられる．

$n$ $x_1$ $y_1$ $r_1$ $x_2$ $y_2$ $r_2$ : $x_n$ $y_n$ $r_n$ $m$ $x1_1$ $y1_1$ $x2_1$ $y2_1$ $x1_2$ $y1_2$ $x2_2$ $y2_2$ : $x1_m$ $y1_m$ $x2_m$ $y2_m$

• $1$ 行目には，図形の数を表す整数 $n (1 ≦ n ≦ 10^5)$ が与えられる．
• $1$ 行目から $n$ 行，各図形の情報を表す $3$ つの整数 $x_i,y_i,r_i (-10^8 ≦ x_i,y_i ≦ 10^8, 1 ≦ r_i ≦ 10^8)$ が与えられる．どの2つの図形についても，それらを構成する点集合同士は共通部分を持たない．
• $n+1$ 行目には，クエリの数を表す整数 $m (1 ≦ m ≦ 10^5)$ が与えられる．
• $n+2$ 行目から $m$ 行，各クエリの2情報を表す $4$ つの整数 $x1_i,y1_i,x2_i,y2_i (-10^8 ≦ x1_i,y1_i,x2_i,y2_i ≦ 10^8)$ が与えられる．この2つの座標は，どの図形の点集合にも含まれないことが保障されている．

出力

1行目から $m$ 行，各クエリについての答えを与えられた順番に改行区切りで出力せよ．最後の行においても改行を行うこと．

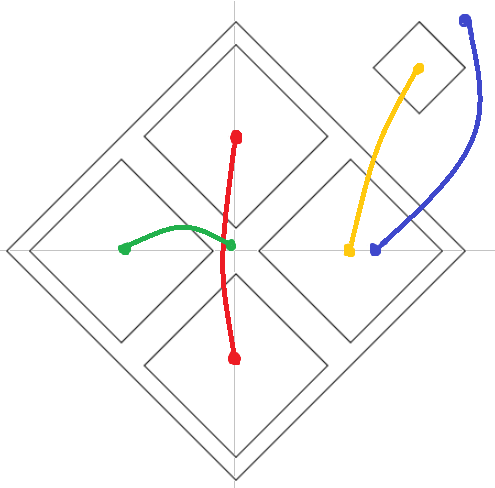
入力例1

5
0 0 1
0 0 5
0 0 9
0 0 13
20 20 1
4
0 0 13 13
0 0 0 7
0 2 0 3
0 0 20 20

出力例1

4
2
0
5

入出力例1を表した図は以下の通りです．

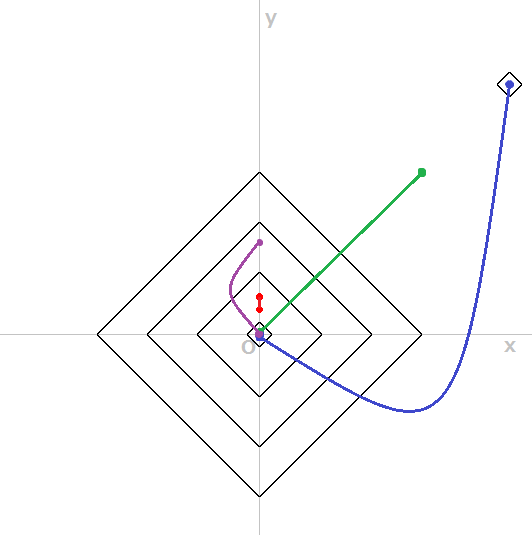
入力例2

6
0 0 10
0 5 4
5 0 4
0 -5 4
-5 0 4
8 8 2
4
0 5 0 -5
6 0 10 10
-5 0 0 0
5 0 8 8

出力例2

2
2
1
3

入出力例2を表した図は以下の通りです．