问题描述

Snuke有一个 $N \times N$ 的棋盘和 $N \times N$ 的方块。

格子边界的每个边都连接有一个插座。也就是说，每个格子的边都连接有 $N$ 个插座，总共有 $4 \times N$ 个插座。这些插座的标签如下所示：

• 格子上边的插座：从左到右依次为 $U1, U2, ..., UN$
• 格子下边的插座：从左到右依次为 $D1, D2, ..., DN$
• 格子左边的插座：从上到下依次为 $L1, L2, ..., LN$
• 格子右边的插座：从上到下依次为 $R1, R2, ..., RN$

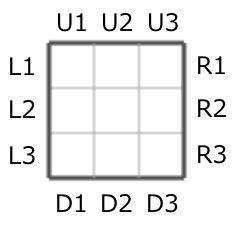
图：插座的标签

Snuke可以将每个插座上的方块插入到插座所连接的正方形中。当一个正方形已经被一个方块占据时，该方块会被推到下一个正方形中，如果下一个正方形也被另一个方块占据，那么该方块也将被推动，以此类推。如果插入方块会导致方块被推出棋盘，Snuke将无法插入方块。方块插入时的行为在样例输入/输出 1 中有详细说明。

Snuke试图从插座中逐个插入 $N \times N$ 个方块，以达到每个正方形都包含一个方块的状态。这里，他必须从插座 $Ui$ 插入 $U_i$ 个方块，从插座 $Di$ 插入 $D_i$ 个方块，从插座 $Li$ 插入 $L_i$ 个方块，从插座 $Ri$ 插入 $R_i$ 个方块。确定是否可以在限制条件下插入方块。如果可以，请按照从插座插入方块的顺序输出插座的标签。

约束条件

• $1≤N≤300$
• $U_i,D_i,L_i$ 和 $R_i$ 是非负整数。
• 所有值 $U_i,D_i,L_i$ 和 $R_i$ 的总和等于 $N \times N$。

部分得分

• 过第一套测试数据（满足 $N≤40$）将获得 $2000$ 分。
• 在没有额外限制的情况下通过测试数据还将额外获得 $100$ 分。

输入

输入以标准输入给出，格式如下：

$N$ $U_1$ $U_2$ $...$ $U_N$ $D_1$ $D_2$ $...$ $D_N$ $L_1$ $L_2$ $...$ $L_N$ $R_1$ $R_2$ $...$ $R_N$

输出

如果可以插入方块，使得每个正方形都包含一个方块，则按照插入方块的顺序逐行输出插座的标签。如果不可能，则输出 NO。如果存在多个解决方案，则可以输出任意一个。

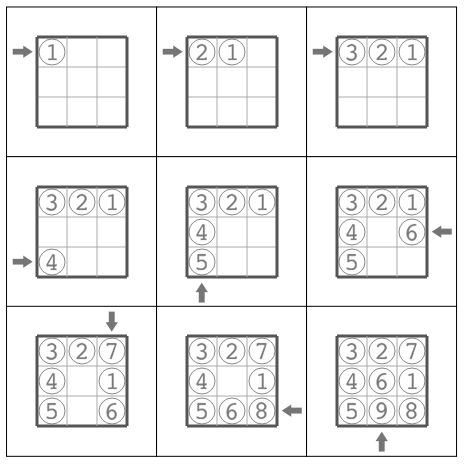
示例输入 1

3
0 0 1
1 1 0
3 0 1
0 1 1

示例输出 1

L1
L1
L1
L3
D1
R2
U3
R3
D2

Snuke可以按照下图所示进行方块的插入。箭头表示方块插入的位置，圆圈表示方块，圆圈中的数字表示在该方块之前和包括该方块在内一共插入了多少方块。

示例输入 2

2
2 0
2 0
0 0
0 0

示例输出 2

NO