问题文

小苹果正在堆叠边长为1的立方体来玩耍。小苹果在地面上画了N个边长为1的正方形，并在第i个正方形上堆叠了Ai个立方体。

小苹果决定给立方体涂上颜色。不涂色与其他立方体或地面接触的面。然而，小苹果开始担心颜料是否足够。因此，她决定先移除K个立方体，然后再涂颜料。在这种情况下，每个正方形上必须至少有一个以上的立方体。

小苹果希望尽可能减少所需颜料的量。请计算涂色面积的最小值。

输入

输入以以下格式从标准输入中给出。

N K A1 A2 ... AN

• 第一行包含两个整数N（1≤N≤105）和K（1≤K≤1014），以空格分隔。表示画在地面上的正方形的数量为N个，要移除的立方体的数量为K个。
• 第二行包含N个整数，以空格分隔，表示每个正方形上堆叠的立方体的数量。其中第i（1≤i≤N）个整数Ai（1≤Ai≤109）表示第i个正方形上堆叠的立方体的数量。保证至少要保留一个以上的立方体在每个正方形上，即ΣAi≥N+K。

输出

输出涂色面积的最小值，输出到一行并以换行符结尾。

输入示例1

7 6
2 3 2 1 2 3 4

输出示例1

35

下图显示了最初堆叠的立方体从正面看的情况。

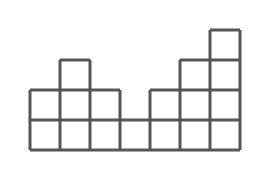
当移除6个立方体时，涂色面积为35。

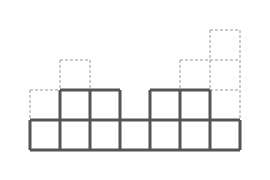
输入示例2

10 919924177
114777581 900857217 199708389 41623648 586160911 824291566 209849198 803644124 355106148 180322764

输出示例2

9307626516