问题描述

想要构建一棵有 $n$ 个叶子的有序二叉树。这棵二叉树的代价定义如下：

$Σ_{i=1}^{n} w_i × depth(i)$

其中，$depth(i)$ 表示二叉树中从左边数第 $i$ 个叶子的深度。$w_i$ 是作为输入给出的权重。请求出代价的最小值。

输入

输入数据从标准输入中按以下格式给出：

$n$ $w_1$ $w_2$ ... $w_n$

• 第一行是一个整数 $n (1≦n≦100,000)$，表示元素的个数。
• 第二行是 $n$ 个整数，表示元素的权重。其中第 $i$ (1≦i≦n)$个元素表示第$i$个元素的权重$w_i(1≦w_i≦1,000)$。

输出

输出满足条件的有序二叉树的最小代价。

部分得分

此问题设有部分得分。

• 对于满足 $n≦100$ 的数据集，如果正确解答则得到 50 分。
• 对于满足 $n≦3,000$ 的数据集，除上述得分外额外再得 50 分。
• 对于未添加任何限制的数据集，除上述得分外额外再得 1 分。

解释

最优二分查找树问题来自 AtCoder Inc.

示例输入 1

6
1 2 3 4 9 3

示例输出 1

53

构造如下图所示的二叉树是最优的。

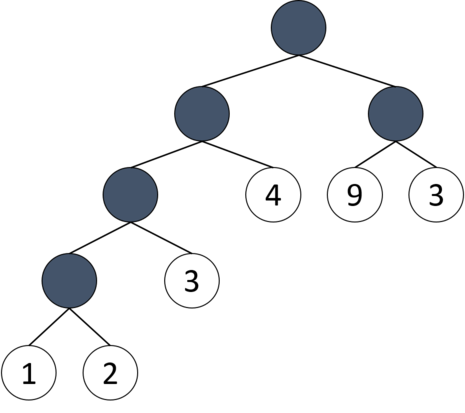
图 1：对应示例输入输出的二叉树

构建这样的二叉树的代价为 53。