問題文

$n$ 個の葉を持つ順序付き二分木を作りたい。 この二分木のコストは以下のように定義される。

$Σ_{i=1}^{n} w_i × depth(i)$

ただし、$depth(i)$ は、二分木における左から $i$ 個目の葉の深さを表す。 $w_i$ は入力として与えられる重みである。 コストの最小値を求めよ。

入力

入力は以下の形式で標準入力から与えられる。

$n$ $w_1$ $w_2$ ... $w_n$

• $1$ 行目には、要素の個数を表す整数 $n (1≦n≦100,000)$ が与えられる。
• $2$ 行目には、要素の重みを表す $n$ 個の整数が与えられる。このうち $i (1≦i≦n)$ 番目の要素は、$i$ 番目の要素の重みを表す $w_i(1≦w_i≦1,000)$ である。

出力

条件を満たす順序付き二分木のコストの最小値を出力せよ。

部分点

この問題には部分点が設定されている。

• $n ≦ 100$ を満たすデータセットに正解した場合は、$50$ 点が与えられる。
• $n ≦ 3,000$ を満たすデータセットに正解した場合は、上記とは別に $50$ 点が与えられる。
• 追加の制約のないデータセットに正解した場合は、上記とは別に $1$ 点が与えられる。

解説

最適二分探索木問題 from AtCoder Inc.

入力例1

6
1 2 3 4 9 3```

### 出力例1

```plain
53

以下の図のような二分木が最適となります。

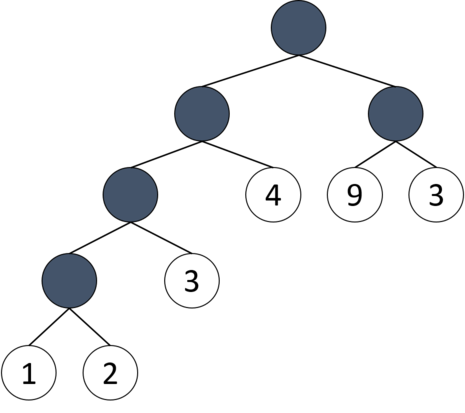
図 1 : サンプル入出力に相当する二分木

このような二分木を作った場合、コストは 53 になります。