题目描述

Snuke 提出了以下问题。

给定长度为 $N$ 的序列 $d$。找到满足以下条件的带标记的顶点为 $1,2,...,N$ 的 $N$ 个顶点的无向图的数量，对 $10^{9}+7$ 取模：

• 图是简单且连通的。
• 顶点 $i$ 的度是 $d_i$。

当 $2 \\leq N, 1 \\leq d_i \\leq N-1, {\\rm Σ} d_i = 2(N-1)$ 时， 可以证明问题的答案是 $\\frac{(N-2)!}{(d_{1} -1)!(d_{2} - 1)! ... (d_{N}-1)!}$。

Snuke 想知道 当 $3 \\leq N, 1 \\leq d_i \\leq N-1, { \\rm Σ} d_i = 2N$ 时的答案。 请在此条件下解决这个问题。

约束条件

• $3 \\leq N \\leq 300$
• $1 \\leq d_i \\leq N-1$
• ${\\rm Σ} d_i = 2N$

部分得分

• 在价值 $200$ 分的测试数据中，$N \\leq 5$。
• 在价值另外 $200$ 分的测试数据中，$N \\leq 18$。
• 在价值另外 $300$ 分的测试数据中，$N \\leq 50$。

输入

从标准输入中按以下格式给出输入：

$N$
$d_1$ $d_2$ $...$ $d_{N}$

输出

输出答案。

示例输入 1

5
1 2 2 3 2

示例输出 1

6

• 如下所示，有六个图：

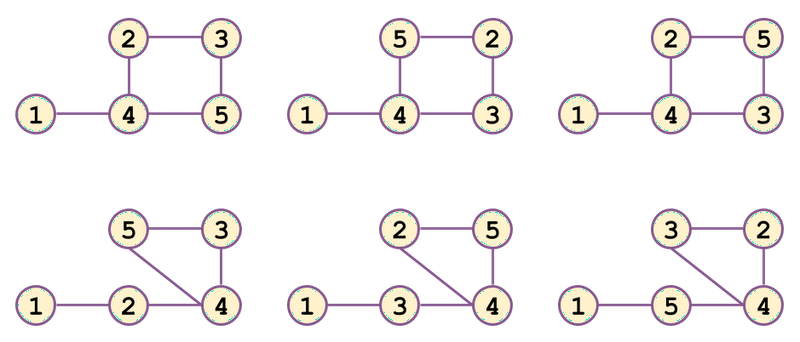
示例输入 2

16
2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3

示例输出 2

555275958

• 请务必将答案对 $10^{9} + 7$ 取模。