問題文

すぬけくんは以下のような問題を考えました。

長さ $N$ の数列 $d$ が与えられます。 以下の条件を満たす頂点に $1,2,...,N$ のラベルがついた $N$ 頂点の無向グラフの数を modulo $10^{9} + 7$ で求めてください。

• グラフは単純かつ連結
• 頂点 $i$ の次数は $d_i$

$2 \\leq N, 1 \\leq d_i \\leq N-1, {\\rm Σ} d_i = 2(N-1)$ を満たす場合 には、この問題の答えは $\\frac{(N-2)!}{(d_{1} -1)!(d_{2} - 1)! ... (d_{N}-1)!}$ で表せることが証明できます。

すぬけくんは $3 \\leq N, 1 \\leq d_i \\leq N-1, { \\rm Σ} d_i = 2N$ を満たす場合 どうなるかが気になっています。 すぬけくんの代わりにこの問題を解いてください。

制約

• $3 \\leq N \\leq 300$
• $1 \\leq d_i \\leq N-1$
• ${ \\rm Σ} d_i = 2N$

部分点

• $200$ 点分のデータセットでは $N \\leq 5$ が成立する
• 別の $200$ 点分のデータセットでは $N \\leq 18$ が成立する
• 別の $300$ 点分のデータセットでは $N \\leq 50$ が成立する

入力

入力は以下の形式で標準入力から与えられる。

$N$ $d_1$ $d_2$ $...$ $d_{N}$

出力

答えを出力せよ。

入力例 1

5
1 2 2 3 2

出力例 1

6

• 以下の図に示されるような $6$ 通りです

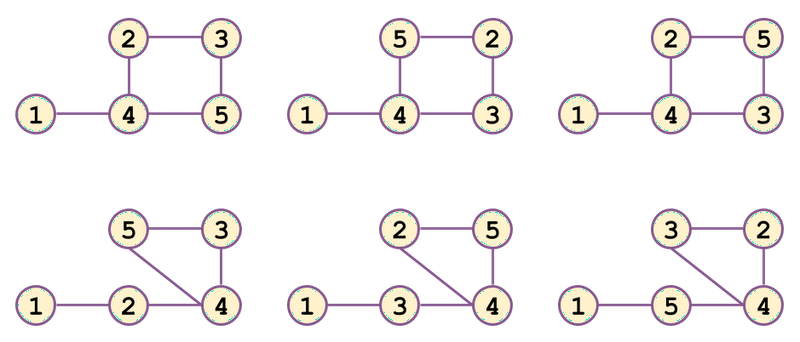
入力例 2

16
2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3

出力例 2

555275958

• $10^{9} + 7$ で割ったあまりを求めてください