Problem Statement

Snuke has come up with the following problem.

You are given a sequence $d$ of length $N$. Find the number of the undirected graphs with $N$ vertices labeled $1,2,...,N$ satisfying the following conditions, modulo $10^{9} + 7$:

• The graph is simple and connected.
• The degree of Vertex $i$ is $d_i$.

When $2 \\leq N, 1 \\leq d_i \\leq N-1, {\\rm Σ} d_i = 2(N-1)$, it can be proved that the answer to the problem is $\\frac{(N-2)!}{(d_{1} -1)!(d_{2} - 1)! ... (d_{N}-1)!}$.

Snuke is wondering what the answer is when $3 \\leq N, 1 \\leq d_i \\leq N-1, { \\rm Σ} d_i = 2N$. Solve the problem under this condition for him.

Constraints

• $3 \\leq N \\leq 300$
• $1 \\leq d_i \\leq N-1$
• ${ \\rm Σ} d_i = 2N$

Partial Scores

• In the test set worth $200$ points, $N \\leq 5$.
• In the test set worth another $200$ points, $N \\leq 18$.
• In the test set worth another $300$ points, $N \\leq 50$.

Input

Input is given from Standard Input in the following format:

$N$ $d_1$ $d_2$ $...$ $d_{N}$

Output

Print the answer.

Sample Input 1

5
1 2 2 3 2

Sample Output 1

6

• There are six graphs as shown below:

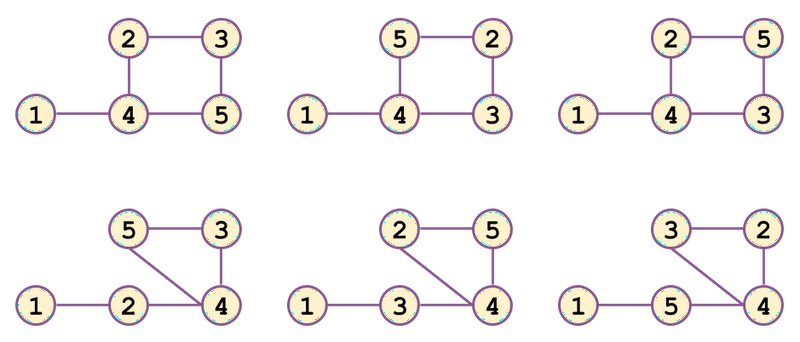
Sample Input 2

16
2 1 3 1 2 1 4 1 1 2 1 1 3 2 4 3

Sample Output 2

555275958

• Be sure to find the answer modulo $10^{9} + 7$.