Problem Statement

Snuke has a sequence $p$, which is a permutation of $(0,1,2, ...,N-1)$. The $i$-th element ($0$-indexed) in $p$ is $p_i$.

He can perform $N-1$ kinds of operations labeled $1,2,...,N-1$ any number of times in any order. When the operation labeled $k$ is executed, the procedure represented by the following code will be performed:

for(int i=k;i<N;i++)
    swap(p\[i\],p\[i-k\]);

He would like to sort $p$ in increasing order using between $0$ and $10^{5}$ operations (inclusive). Show one such sequence of operations. It can be proved that there always exists such a sequence of operations under the constraints in this problem.

Constraints

• $2 \\leq N \\leq 200$
• $0 \\leq p_i \\leq N-1$
• $p$ is a permutation of $(0,1,2,...,N-1)$.

Partial Scores

• In the test set worth $300$ points, $N \\leq 7$.
• In the test set worth another $400$ points, $N \\leq 30$.

Input

Input is given from Standard Input in the following format:

$N$ $p_0$ $p_1$ $...$ $p_{N-1}$

Output

Let $m$ be the number of operations in your solution. In the first line, print $m$. In the $i$-th of the following $m$ lines, print the label of the $i$-th executed operation. The solution will be accepted if $m$ is at most $10^5$ and $p$ is in increasing order after the execution of the $m$ operations.

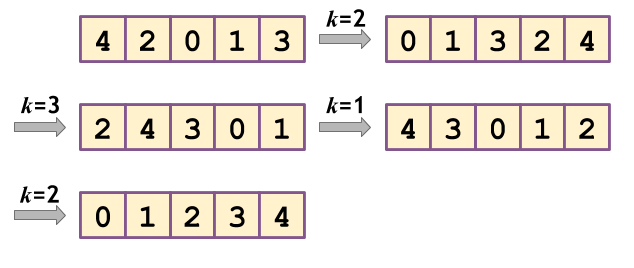
Sample Input 1

5
4 2 0 1 3

Sample Output 1

4
2
3
1
2

• Each operation changes $p$ as shown below:

Sample Input 2

9
1 0 4 3 5 6 2 8 7

Sample Output 2

11
3
6
1
3
5
2
4
7
8
6
3