题目描述

给定二维平面上的 $N$ 个点 $(x_i,y_i)$。考虑一个由这 $N$ 个点构成的子集 $S$，使它们形成一个凸多边形。这里，我们说一个点集 $S$ 形成了一个凸多边形，当存在一个面积大于 $0$ 的凸多边形，他们的顶点与点集 $S$ 相同，并且多边形内的所有角度都严格小于 $180°$。

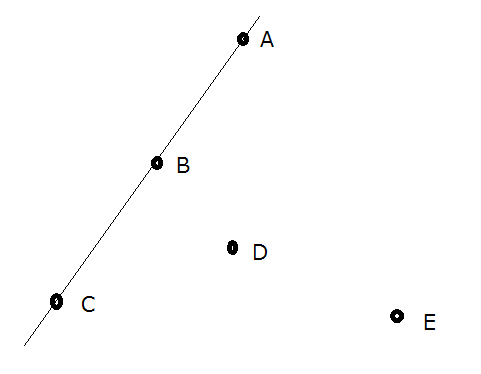
例如，在上面的图中，{$A,C,E$} 和 {$B,D,E$} 形成凸多边形；{$A,C,D,E$}、{$A,B,C,E$}、{$A,B,C$}、{$D,E$} 和 {} 不是。

对于给定的集合 $S$，设 $n$ 为 $N$ 个点中在 $S$ 的凸包（包括边界和顶点）内的点的个数。那么，我们将 $S$ 的 得分 定义为 $2^{n-|S|}$。

计算所有可能形成凸多边形的集合 $S$ 的得分之和，并将其对 $998244353$ 取模。

约束条件

• $1≤N≤200$
• $0≤x_i,y_i<10^4 (1≤i≤N)$
• 若 $i≠j$，$x_i≠x_j$ 或 $y_i≠y_j$。
• $x_i$ 和 $y_i$ 为整数。

输入格式

输入通过标准输入给出，格式如下：

$N$ $x_1$ $y_1$ $x_2$ $y_2$ $:$ $x_N$ $y_N$

输出格式

打印得分之和对 $998244353$ 取模的结果。

示例输入1

4
0 0
0 1
1 0
1 1

示例输出1

5

总共有五个可能的集合 $S$，其中四个形成三角形，一个形成正方形。它们的得分都是 $2^0=1$，因此答案是 $5$。

示例输入2

5
0 0
0 1
0 2
0 3
1 1

示例输出2

11

总共有三个得分为 $1$ 的"三角形"，两个得分为 $2$ 的"三角形"，以及一个得分为 $4$ 的"三角形"。因此，答案是 $11$。

示例输入3

1
3141 2718

示例输出3

0

没有可能的集合 $S$，所以答案是 $0$。