问题描述

在 $xy$ 平面上有一个矩形，其左下角坐标为 $(0, 0)$，右上角坐标为 $(W, H)$。矩形的边与 $x$ 轴或 $y$ 轴平行。初始时，矩形内部的所有区域都被涂成白色。

Snuke 在矩形内绘制了 $N$ 个点。第 $i$ 个点（$1 ≤ i ≤ N$）的坐标为 $(x_i, y_i)$。

然后，对于每个 $1 ≤ i ≤ N$，他将在以下四个区域中的一个区域绘制成黑色：

• 矩形内满足 $x < x_i$ 的区域
• 矩形内满足 $x > x_i$ 的区域
• 矩形内满足 $y < y_i$ 的区域
• 矩形内满足 $y > y_i$ 的区域

找到 Snuke 绘制结束后矩形内白色区域的最长周长。

约束条件

• $1 ≤ W, H ≤ 10^8$
• $1 ≤ N ≤ 3 × 10^5$
• $0 ≤ x_i ≤ W$ ($1 ≤ i ≤ N$)
• $0 ≤ y_i ≤ H$ ($1 ≤ i ≤ N$)
• $W$、$H$（增加于21:32）、$x_i$ 和 $y_i$ 均为整数。
• 若 $i ≠ j$，则 $x_i ≠ x_j$ 且 $y_i ≠ y_j$。

输入

输入以以下格式从标准输入给出：

$W$ $H$ $N$ $x_1$ $y_1$ $x_2$ $y_2$ : $x_N$ $y_N$

输出

打印 Snuke 绘制结束后矩形内白色区域的最长周长。

示例输入 1

10 10 4
1 6
4 1
6 9
9 4

示例输出 1

32

在本例中，通过按照以下方式绘制矩形可以得到最大周长为 $32$ 的白色区域：

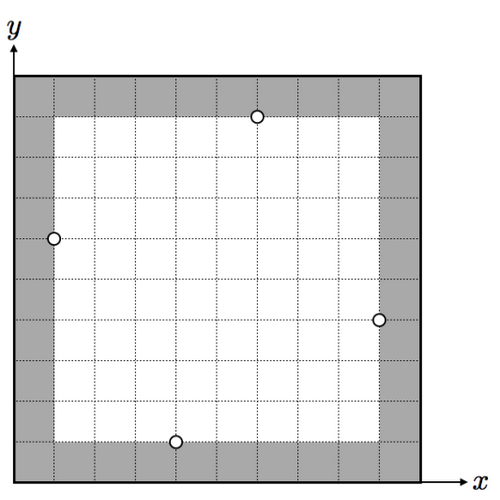
示例输入 2

5 4 5
0 0
1 1
2 2
4 3
5 4

示例输出 2

12

示例输入 3

100 100 8
19 33
8 10
52 18
94 2
81 36
88 95
67 83
20 71

示例输出 3

270

示例输入 4

100000000 100000000 1
3 4

示例输出 4

399999994