题目描述

有一天，小鹿 AtCoDeer 找到了一个简单的图（即没有自环和重复边的图），它有 $N$ 个顶点和 $M$ 条边，并把它带回了家。顶点编号从 $1$ 到 $N$，并且彼此可区分，边由 $(a_i, b_i) (1≦i≦M)$ 表示。

他将图中的每条边涂上 $K$ 种颜色之一。因为他有足够的颜料供应，所以可以使用相同的颜色来涂多条边。

这个图由一种特殊的材料制成，具有一种奇怪的性质。他可以选择一个简单的循环（即没有重复顶点的循环），并沿着选择的循环对颜色进行循环移位。更正式地说，设 $e_1$, $e_2$, $...$, $e_a$ 是按顺序经过的循环中的边，则可以同时执行以下操作：用 $e_1$ 的当前颜色涂上 $e_2$，用 $e_2$ 的当前颜色涂上 $e_3$，依此类推，最后用 $e_{a}$ 的当前颜色涂上 $e_1$。

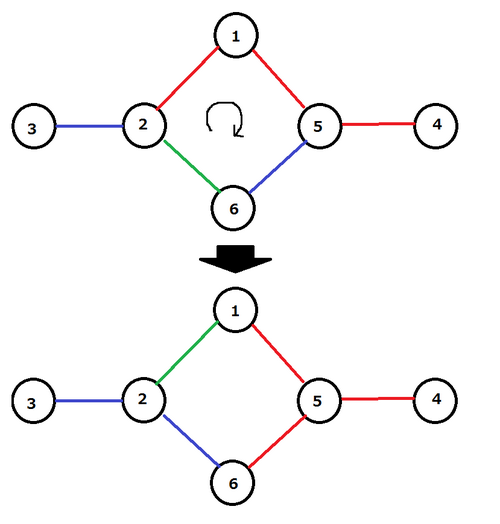
图 $1$: 循环移位的示例

如果通过有限次循环移位，可以将边的涂色方式 $A$ 转化为 $B$，则认为两种涂色方式 $A$ 和 $B$ 是相同的。找出涂色的方式数量。由于这个数量可能非常大，将答案对 $10^9+7$ 取模后输出。

约束条件

• $1≦N≦50$
• $1≦M≦100$
• $1≦K≦100$
• $1≦a_i,b_i≦N (1≦i≦M)$
• 图中没有自环和重复边。

输入

输入从标准输入读入，输入格式如下：

$N$ $M$ $K$ $a_1$ $b_1$ $a_2$ $b_2$ $:$ $a_M$ $b_M$

输出

输出涂色方式的数量，对 $10^9+7$ 取模后输出。

示例输入1

4 4 2
1 2
2 3
3 1
3 4

示例输出1

8

示例输入2

5 2 3
1 2
4 5

示例输出2

9

示例输入3

11 12 48
3 1
8 2
4 9
5 4
1 6
2 9
8 3
10 8
4 10
8 6
11 7
1 8

示例输出3

569519295