有数个大头钉在二维平面上，有四个人从不同的角度观察它们，重叠的点视为一个，是否可能有一个人观察到的大头钉数量远多余其他人？

让我们把大头钉的位置简化为二维坐标上的点。四个人观察的角度如下：

• A 从左往右观察。即所有 $y$ 坐标相同的点是重叠的。
• B 从左下往右上观察。即所有 $x$ 坐标与 $y$ 坐标相减的值相同的点是重叠的。
• C 从下往上观察。即所有 $x$ 坐标相同的点是重叠的。
• D 从右下往左上观察。即所有 $x$ 坐标与 $y$ 坐标相加的值相同的点是重叠的。

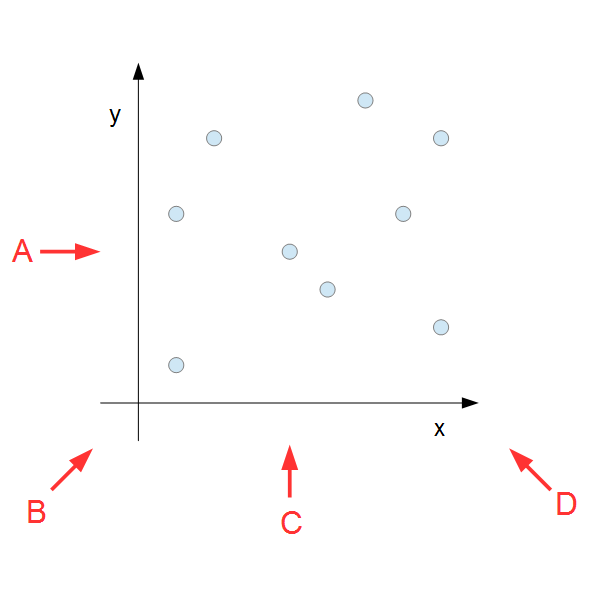
令 A, B, C, D 观察到的大头针数量为 $a, b, c, d$，你需要构造一组大头针的排布，满足以下一些条件：

• $d \geq 10 \times \max\{a, b, c\}$
• 大头钉的数量不多于 $10^5$ 个。
• 大头钉的坐标均为 $[0, 10^9]$ 内的整数。
• 不存在两个坐标相同的大头钉。

没有输入，直接输出一组解。