题目描述

Takahashi 收到了一个有 $N$ 个顶点的无向图，编号为 $1$，$2$，...，$N$。图中的边由 $(u_i, v_i)$ 表示。此图中没有自环和多重边。

基于这个图，Takahashi 现在正在构建一个有 $N^2$ 个顶点的新图，其中每个顶点都标有一对整数 $(a, b)$（$1 \leq a \leq N$，$1 \leq b \leq N$）。新图中的边是根据以下规则生成的：

• 如果原始图中同时存在两条边：一条连接顶点$a$ 和 $a'$，另一条连接顶点 $b$ 和 $b'$，则在新图中连接顶点 $(a, b)$ 和 $(a', b')$。

这个新图中有多少个连通分量？

约束条件

• $2 \leq N \leq 100,000$
• $0 \leq M \leq 200,000$
• $1 \leq u_i < v_i \leq N$
• 不存在不同整数$i$和$j$使得$u_i = u_j$且$v_i = v_j$。

输入

从标准输入读取的输入数据格式如下：

$N$ $M$ $u_1$ $v_1$ $u_2$ $v_2$ ： $u_M$ $v_M$

输出

打印由Takahashi构造的图中的连通分量的数量。

示例 1

3 1
1 2

输出 1

7

Takahashi构建的图如下：

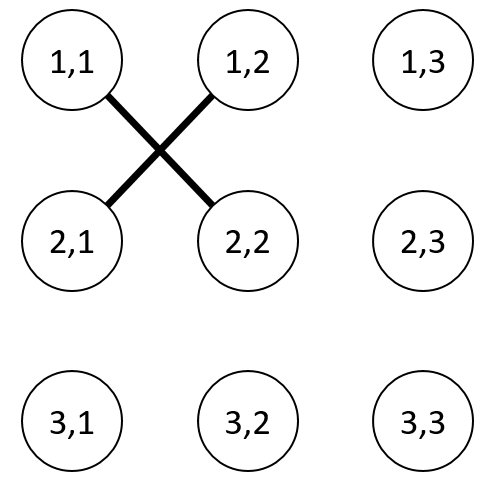
示例 2

7 5
1 2
3 4
3 5
4 5
2 6

输出 2

18