問題文

高橋君は，$N$ 頂点 $1$, $2$, ..., $N$ からなる無向グラフをもらいました． このグラフの辺は $(u_i, v_i)$ で表されます． このグラフには，自己辺や多重辺は存在しません．

高橋君は，このグラフをもとに，$N^2$ 頂点 $(a, b)$ ($1 \\leq a \\leq N$, $1 \\leq b \\leq N$) からなるグラフを作ることにしました． このグラフの辺は，次の規則で定まります．

• 元のグラフにおいて $a$ と $a'$ の間および $b$ と $b'$ の間の両方に辺があるとき，またそのときに限り，$(a, b)$ と $(a', b')$ の間に辺を張る．

このようにして作ったグラフの連結成分の個数を求めてください．

制約

• $2 \\leq N \\leq 100,000$
• $0 \\leq M \\leq 200,000$
• $1 \\leq u_i < v_i \\leq N$
• $u_i = u_j$ かつ $v_i = v_j$ を満たすような異なる $i, j$ の組は存在しない

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$ $u_1$ $v_1$ $u_2$ $v_2$ : $u_M$ $v_M$

出力

高橋君の作ったグラフの連結成分の個数を出力せよ．

入力例 1

3 1
1 2

出力例 1

7

高橋君の作ったグラフは下のようになります．

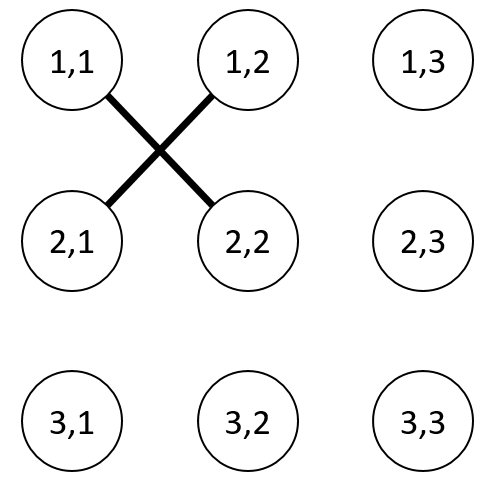
入力例 2

7 5
1 2
3 4
3 5
4 5
2 6

出力例 2

18