题目描述

有 $N$ 位选手参加了一场比赛。在淘汰赛中，需要进行 $N-1$ 场比赛。由于某些原因，比赛对于每个选手来说可能并不公平。也就是说，为了赢得冠军，每个选手必须进行的比赛次数可能是不同的。以下是正式描述的比赛结构。

每场比赛之后，总有一个胜利者和一个失败者。最后剩下的选手被宣布为冠军。

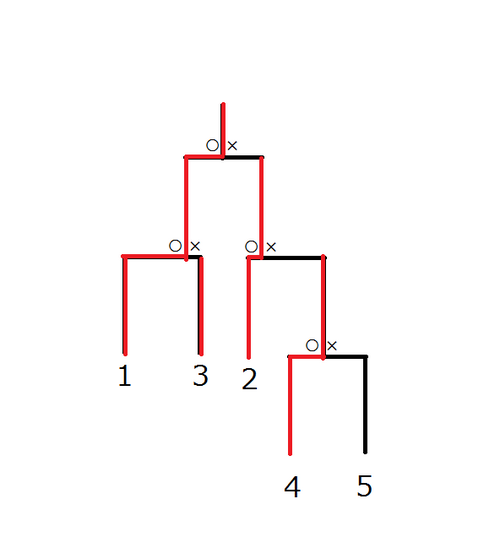
图：比赛的示例

为了方便起见，选手编号为 $1$ 到 $N$。编号为 $1$ 的选手是冠军，编号为 $i(2≤i≤N)$ 的选手在与编号为 $a_i$ 的选手进行比赛中失败。

我们将定义比赛的深度为在所有选手中为了赢得冠军而必须进行的最大比赛次数。

找到比赛的最小可能深度。

比赛结构的正式描述如下。在第 $i$ 场比赛中，以下其中之一发生：

• 两个预定的选手进行比赛
• 一个预定的选手和第 $j$ 场比赛的胜利者进行比赛，其中 $j(j<i)$ 是预定的
• 第 $j$ 场比赛和第 $k$ 场比赛的胜利者进行比赛，其中 $j$ 和 $k$ $(j,k<i, j≠k)$ 是预定的

只要无论比赛的结果如何，已经在比赛中输掉的选手不会再参加比赛，这样的结构就是有效的比赛结构。

约束条件

• $2 ≤ N ≤ 10^5$
• $1 ≤ a_i ≤ N(2 ≤ i ≤ N)$
• 输入保证一致（即，至少存在一个与给定信息相匹配的比赛）。

输入

输入以以下格式从标准输入给出：

$N$ $a_2$ : $a_N$

输出

打印比赛的最小可能深度。

示例 1

5
1
1
2
4

输出 1

3

下图中的比赛和比赛结果与给定的信息一致：

• 在第一场比赛中，选手 $4$ 和 $5$ 进行比赛，选手 $4$ 获胜。
• 在第二场比赛中，选手 $2$ 和 $4$ 进行比赛，选手 $2$ 获胜。
• 在第三场比赛中，选手 $1$ 和 $3$ 进行比赛，选手 $1$ 获胜。
• 在第四场比赛中，选手 $1$ 和 $2$ 进行比赛，选手 $1$ 获胜。

这个比赛的深度是 $3$，因为选手 $5$ 必须进行三场比赛才能赢得冠军。不存在深度小于等于 $2$ 的与给定信息相匹配的比赛，因此输出应为 $3$。

示例 2

7
1
2
1
3
1
4

输出 2

3

示例 3

4
4
4
1

输出 3

3