题目描述

有一棵 $N$ 个顶点的树。顶点从 $1$ 到 $N$ 编号。对于每个 $1 ≤ i ≤ N-1$，第 $i$ 条边连接顶点 $a_i$ 和 $b_i$。所有边的长度为 $1$。

Snuke 喜欢其中一些顶点。他喜欢的顶点的信息以一个长度为 $N$ 的字符串 $s$ 给出。对于每个 $1 ≤ i ≤ N$，若 Snuke 喜欢顶点 $i$，则 $s_i$ 为 1，否则为 0。

初始时，所有顶点都是白色的。Snuke 将执行以下操作一次：

• 选择一个他喜欢的顶点 $v$，和一个非负整数 $d$。然后，将所有距离 $v$ 不超过 $d$ 的顶点涂成黑色。

找出操作后可能的顶点颜色组合的数量。

约束条件

• $2 ≤ N ≤ 2×10^5$
• $1 ≤ a_i, b_i ≤ N$
• 给定的图是一棵树。
• $|s| = N$
• $s$ 由 0 和 1 组成。
• $s$ 中至少包含一个 1。

分数说明

• 在价值 $1300$ 分的测试集中，$s$ 仅包含 1。

输入

输入以以下格式从标准输入给出：

$N$ $a_1$ $b_1$ $a_2$ $b_2$ $:$ $a_{N - 1}$ $b_{N - 1}$ $s$

输出

打印操作后可能的顶点颜色组合的数量。

示例 1

4
1 2
1 3
1 4
1100

输出 1

4

有以下四种可能的顶点颜色组合：

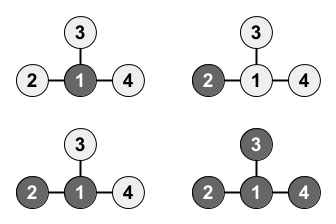
示例 2

5
1 2
1 3
1 4
4 5
11111

输出 2

11

此示例满足部分得分的额外约束条件。

示例 3

6
1 2
1 3
1 4
2 5
2 6
100011

输出 3

8