Problem Statement

There is a tree with $N$ vertices. The vertices are numbered $1$ through $N$. For each $1 ≤ i ≤ N - 1$, the $i$-th edge connects vertices $a_i$ and $b_i$. The lengths of all the edges are $1$.

Snuke likes some of the vertices. The information on his favorite vertices are given to you as a string $s$ of length $N$. For each $1 ≤ i ≤ N$, $s_i$ is 1 if Snuke likes vertex $i$, and 0 if he does not like vertex $i$.

Initially, all the vertices are white. Snuke will perform the following operation exactly once:

• Select a vertex $v$ that he likes, and a non-negative integer $d$. Then, paint all the vertices black whose distances from $v$ are at most $d$.

Find the number of the possible combinations of colors of the vertices after the operation.

Constraints

• $2 ≤ N ≤ 2×10^5$
• $1 ≤ a_i, b_i ≤ N$
• The given graph is a tree.
• $|s| = N$
• $s$ consists of 0 and 1.
• $s$ contains at least one occurrence of 1.

Partial Score

• In the test set worth $1300$ points, $s$ consists only of 1.

Input

The input is given from Standard Input in the following format:

$N$ $a_1$ $b_1$ $a_2$ $b_2$ $:$ $a_{N - 1}$ $b_{N - 1}$ $s$

Output

Print the number of the possible combinations of colors of the vertices after the operation.

Sample Input 1

4
1 2
1 3
1 4
1100

Sample Output 1

4

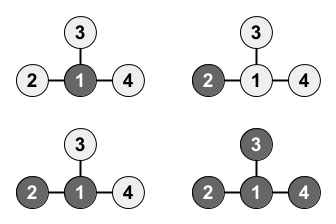
The following four combinations of colors of the vertices are possible:

Sample Input 2

5
1 2
1 3
1 4
4 5
11111

Sample Output 2

11

This case satisfies the additional constraint for the partial score.

Sample Input 3

6
1 2
1 3
1 4
2 5
2 6
100011

Sample Output 3

8