問題文

$N$ 頂点の木があり、頂点には $1 ～ N$ の番号がついています。$N - 1$ 本の辺について、$i (1≦i≦N-1)$ 本目の辺は頂点 $A_i$ と頂点 $B_i$ を繋いでいます。

この木の直径を $K$ 以下にするために削除する必要のある頂点数の最小値を求めてください。 ただし、頂点を削除した後のグラフは連結になっていなければなりません。

木の直径とは、$2$ つの頂点間の距離の最大値のことを指します。$2$ つの頂点間の距離とは、$2$ つの頂点を結ぶパスに含まれる辺の本数を指します。

制約

• $2≦N≦2000$
• $1≦K≦N-1$
• $1≦A_i≦N, 1≦B_i≦N$
• 与えられるグラフは木である。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $K$ $A_1$ $B_1$ $A_2$ $B_2$ : $A_{N-1}$ $B_{N-1}$

出力

直径を $K$ 以下にするために削除する必要のある頂点数の最小値を出力せよ。

入力例 1

6 2
1 2
3 2
4 2
1 6
5 6

出力例 1

2

木の構造は図のとおりです。 頂点 $5,6$ を削除すると直径を $2$ に出来ます。

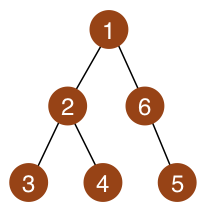
入力例 2

6 5
1 2
3 2
4 2
1 6
5 6

出力例 2

0

すでに直径が $K$ 以下なので、頂点を削除する必要はありません。