题目描述

日本动物女孩图书馆（JAG Library）以其长长的书架而闻名。它包含了从左到右编号为1到N的N本书。第i本书的重量为$w_i$。

一天，调皮的狐狸Jiro打乱了书架上的书的顺序！现在的顺序变成了从左到右的排列$b_1, \ldots, b_N$。JAG Library的图书管理员Fox Hanako必须恢复原始的顺序。她可以通过执行下面描述的操作A或操作B来重新排列书的排列$p_1, \cdots, p_N$，其中$l$和$r$是满足$1 \le l < r \le N$的任意两个整数。

操作A：

• A-1. 从书架上移除$p_l$。
• A-2. 将$p_{l+1}$和$p_r$之间的书向左移动。
• A-3. 将$p_l$插入到$p_r$的右侧。

操作B：

• B-1. 从书架上移除$p_r$。
• B-2. 将$p_l$和$p_{r-1}$之间的书向右移动。
• B-3. 将$p_r$插入到$p_l$的左侧。

下图演示了应用操作A和B后$p=(3,1,4,5,2,6)$，$l=2$，$r=5$的书的顺序。

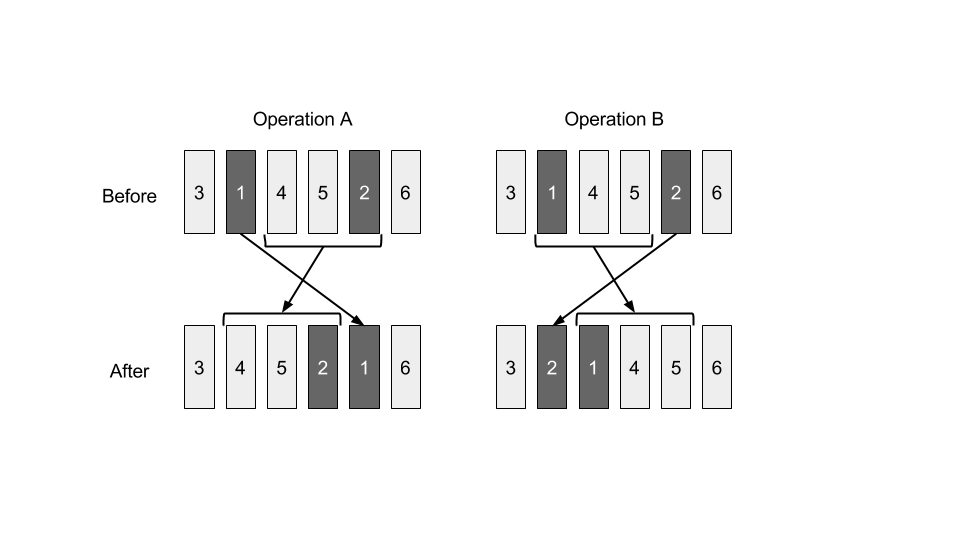
由于书很重，操作A需要$\\sum_{i=l+1}^{r} w_{p_i} + C \times (r-l) \times w_{p_l}$单位的工作量，操作B需要$\\sum_{i=l}^{r-1} w_{p_i} + C \times (r-l) \times w_{p_r}$单位的工作量，其中$C$是一个给定的正整数。

Hanako必须通过反复执行这些操作来恢复初始顺序$b_1, \\cdots, b_N$。找到实现此目标的最小工作量总和。

输入

输入由单个测试用例组成，格式如下。

$N \\ C$ $b_1 \\ w_{b_1}$ $\\vdots$ $b_N \\ w_{b_N}$

第一行包含两个整数$N$和$C \\ (1 \\le N \\le 10^5, 1 \\le C \\le 100)$。第$(i+1)$行包含两个整数$b_i$和$w_{b_i} \\ (1 \\le b_i \\le N, 1 \\le w_{b_i} \\le 10^5)$。序列$(b_1, \\ldots, b_N)$是$(1, \\ldots, N)$的一个排列。

输出

在一行中打印最小工作量总和。

示例输入1

3 2
2 3
3 4
1 2

示例输出1

15

通过$l=1$，$r=3$进行操作B，即先移除书1，然后将其插入到书2的左侧是最优解。它的工作量为$(3 + 4) + 2 \times 2 \times 2 = 15$单位。

示例输入2

3 2
1 2
2 3
3 3

示例输出2

0

示例输入3

10 5
8 3
10 6
5 8
2 7
7 6
1 9
9 3
6 2
4 5
3 5

示例输出3

824