问题描述

树是一种由顶点和连接它们的边构成的结构，称为"图"，当顶点的数量为$N$时，边的数量为$N-1$，每个顶点都通过边与其他所有顶点间接或直接相连。

在本问题中，顶点有$N$个，从1到$N$进行编号。

给定一棵树，求以下操作得到的所有序列中字典序最小的序列。

1. 选择顶点1。
2. 在已选择的顶点和与之相连的顶点中选择一个尚未选择的顶点，直到没有尚未选择的顶点为止。
3. 构建一个按顺序排列的顶点编号的序列。

对于长度为$N$的序列$A=\{a_1,a_2,...,a_N\}$和$B=\{b_1,b_2,...,b_N\}$，按字典顺序$A$小于$B$是指：

• 存在$k(1≦k≦N)$，使得对于$i < k$，$a_i\ =\ b_i$；对于$i = k$，$a_i < b_i$。

---

输入

输入从标准输入读取，并具有以下格式。

$N$

$a_1\ b_1$

$a_2\ b_2$

：

$a_{N-1}\ b_{N-1}$

• 第1行为表示树的顶点数量的整数$N (2≦N≦10^5)$。
• 第2行到第$N-1$行表示树的边的信息。其中第$i (1≦i≦N-1)$行给出连接顶点$a_i$和顶点$b_i$的边的两个整数$a_i$和$b_i$。
• 连接$N$个顶点的$N-1$条边可以构成一棵树。

部分分

此问题设有部分分。

• 对于50个测试用例，满足$1 ≦ N ≦ 3,000$。

输出

在第1行上，以空格分隔输出从给定的树构建的字典顺序最小的序列。

请不要忘记换行符。另外，请勿在行末添加额外的空格。

---

示例输入1

4
1 3
1 4
2 3

示例输出1

1 3 2 4

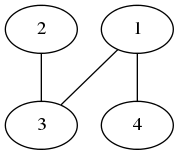
这是问题描述中的图。

首先选择顶点1。

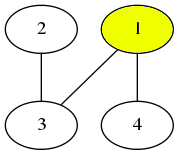
然后选择顶点3。请注意，顶点2未与已选择的顶点（在本例中，仅顶点1）通过边相连，因此无法选择。

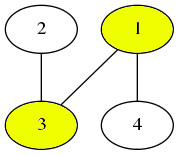
然后选择顶点2。

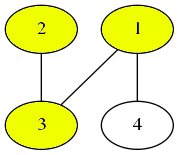
最后选择顶点4。

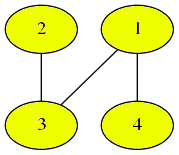
按照选择的顶点编号进行排序，得到序列$1$ $3$ $2$ $4$。不存在比这个序列字典序更小的选择方式。

---

示例输入2

6
1 2
2 3
2 6
6 4
1 5

示例输出2

1 2 3 5 6 4

---

示例输入3

7
1 5
5 2
5 3
5 7
5 6
6 4

示例输出3

1 5 2 3 6 4 7

---