問題文

木とは、頂点とそれを結ぶ辺からなる構造「グラフ」の $1$ 種で、頂点の数を $N$ 個とすると、辺は $N-1$ 本あり、どの頂点も他の全ての頂点に辺で間接・直接的につながっています。

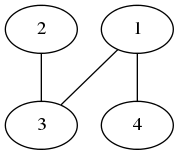
この問題では、頂点は $N$ 個あり、$1$ から $N$ まで番号付けられています。

木が与えられたとき、以下の操作で作られる数列のうち、辞書順で最小のものを出力してください。

1. 頂点1を選ぶ。
2. 今まで選ばれた頂点と辺で結ばれている頂点のうち、まだ選ばれていない頂点を1つ選ぶ、という操作を選ばれていない頂点が無くなるまで繰り返す。
3. 頂点の番号を選ばれた順に並べた数列を作る。

ただし、長さ $N$ の列 $A=\\{a_1,a_2, ...,a_N\\}$ と $B=\\{b_1,b_2, ...,b_N\\}$ に対し、辞書順で $A$ が $B$ より小さいとは、

• $i < k$ で $a_i$=$b_i$
• $i = k$ で $a_i$<$b_i$

となるような $k(1≦k≦N)$ が存在するということです。

---

入力

入力は以下の形式で標準入力から与えられる。

$N$ $a_1$ $b_1$ $a_2$ $b_2$ ： $a_{N-1}$ $b_{N-1}$

• $1$ 行目には、木の頂点の数を表す整数 $N (2 ≦ N ≦ 10^5)$ が与えられる。
• $2$ 行目から $N-1$ 行には、木の辺の情報が与えられる。このうち $i (1 ≦ i ≦ N-1)$ 行目には頂点 $a_i$ と頂点 $b_i$ を結ぶ辺があることを表す $2$ つの整数 $a_i$ , $b_i$ が与えられる。
• $N-1$ 本の辺で結ばれる $N$ 個の頂点は木を成すことが保障される。

部分点

この問題には部分点が設定されている。

• $50$ 点分のテストケースにおいて、 $1 ≦ N ≦ 3,000$ を満たす。

出力

$1$ 行目に、与えられた木から作られる辞書順で最小の数列を空白区切りで出力せよ。

行末の改行を忘れないこと。また，行末に余分な空白を入れてはならない。

---

入力例1

4
1 3
1 4
2 3

出力例1

1 3 2 4

問題文中の図の木です。

まず、初めに頂点 $1$ を選びます。

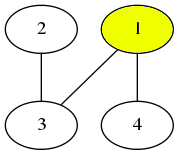
次に、頂点 $3$ を選びます。頂点 $2$ は今まで選んだ頂点(この場合、頂点 $1$ のみ)と辺で結ばれていないので、選ぶことができないことに注意してください。

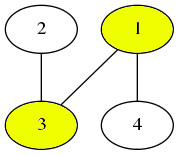
次に、頂点 $2$ を選びます。

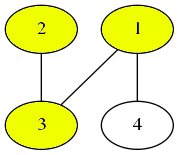
次に、頂点 $4$ を選びます。

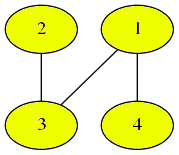
頂点の番号を選んだ順に並べると、$1$ $3$ $2$ $4$ となります。この列より辞書順で小さい選び方は存在しません。

---

入力例2

6
1 2
2 3
2 6
6 4
1 5

出力例2

1 2 3 5 6 4

---

入力例3

7
1 5
5 2
5 3
5 7
5 6
6 4

出力例3

1 5 2 3 6 4 7

---