问题描述

高桥现在在曼哈顿。曼哈顿被南北和东西的道路划分为方块，每条道路都很长，因此南北和东西的路都会相交，在交叉点处形成十字路口。此外，南北和东西的道路不会相互交叉。

我们用编号为$x$的南北道路和编号为$y$的东西道路的交叉点表示为$(x,y)$。

高桥打算从交叉点$(x_1,y_1)$到交叉点$(x_2,y_2)$去。请问，他至少要经过多少个交叉点？经过的交叉点包括交叉点$(x_1,y_1)$和交叉点$(x_2,y_2)$。

请编写一个程序来计算高桥需要经过的交叉点数。

输入

输入通过标准输入给出，格式如下。

$x_1$ $y_1$ $x_2$ $y_2$

• 第1行是高桥最初所在的交叉点的位置$x_1, y_1 (1 ≦ x_1, y_1 ≦ 100,000)$。
• 第2行是高桥目的地交叉点的位置$x_2, y_2 (1 ≦ x_2, y_2 ≦ 100,000)$。
• 保证$(x_1, y_1) ≠ (x_2, y_2)$，即目的地的交叉点与最初所在的交叉点不同。

输出

输出交叉点数的最小值，即高桥从最初的交叉点到目的地交叉点所需要经过的最少交叉点数。

末尾的换行符不要忘记输出。

输入例子1

3 3
2 5

输出例子1

4

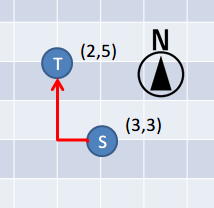
S表示最初的交叉点，T表示目的地的交叉点。

例如，通过$(3,3) → (2,3) → (2,4) → (2,5)$可以经过4个交叉点到达目的地。无法通过少于4个交叉点到达目的地。

输入例子2

1 2
1 1

输出例子2

2

直接通过$(1,2) → (1,1)$是最优的。

输入例子3

20 40
32 64

输出例子3

37