描述

给定一张大小为$w\*h$的二值图像。在这张图像上进行了绘画，但有人恶作剧地将部分白色和黑色像素值互换了。为了恢复原始图像，我查阅了各种文献，并决定采用以下方法：

• 假设噪声（被恶作剧修改的像素）很少。
• 将被恶作剧修改后的图像在位置(x,y)的像素值记为Y(x,y)。
• 将恢复后的图像在位置(x,y)的像素值记为X(x,y)。
• 将位置(x,y)的4邻域（上下左右）记为d(x,y)。
• 考虑方程。
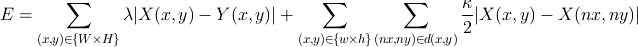• 选取使E最小化的恢复后图像是最好的选择。
• 顺便说一句，方程的前半部分起到保持图像不变化的作用，后半部分则起到避免颜色剧烈变化的作用。

由于方法已经确定，我决定编写程序来恢复图像。

输入

输入包含多个测试用例。输入以4个0组成的行来表示输入的结束。每个测试用例的格式如下：

h w λ κ
Y(1,1)Y(2,1)...Y(w,1)
Y(1,2)Y(2,2)...Y(w,2)
  ...
Y(1,h)Y(2,h)...Y(w,h)

• 1<=h,w<=50
• 0.000<λ,κ<=1.000

λ和κ以0.001的增量给出。

每个测试用例的第一行包含两个整数h和w以及两个实数λ和κ。其中，w和h分别表示图像的宽度和高度，λ和κ表示要最小化的目标函数E的参数。

接下来的h行包含由.和#构成的长度为w的字符串。Y(x,y)是修改后的图像在位置(x,y)的像素值，.表示0，#表示1。

保证每个文件中的测试用例数不超过300个。并且每个文件中$w\*h$的总和不超过8000。

输出

对于每个测试用例，输出一个行表示使E最小的值，并在接下来的h行以与输入相同的格式输出分配给该最小值的像素。允许的误差为绝对误差或相对误差，最多到$10^{-6}$。如果有多个分配产生相同的最小值，则输出任意一个即可。

示例输入

10 10 0.4000 0.20
.##...###.
.##.####..
.######...
.#.#.####.
######....
##.##.....
....#.....
..####.#..
.#####.##.
.#####.##.
25 38 0.5 0.24
...........#...............#..........
...........###..........####..........
....##.....#####.......####...........
.....##.....###############.....##....
............#####.###.#####......#....
............#########.####............
.....##......#########.###............
....##......#####.#########........#..
....#......##.##..####..####..........
.......#...###########.#####...#......
.......##.##################..##......
........#####.####.##.######.##.......
..........####################........
.........##.##..########..#####.......
.......######....##..#....###.##......
......###.####...##.##..#####.##.#....
....###..##..#...#####..#..########...
..####..###.....#######......#######..
...#######......#######........###....
..####.........##.######........###...
...............###...###..............
..............#######..#...#...##.....
.........#....##########...#....#.....
..#.....##.....########...............
...............########...............
0 0 0 0

示例输出

11.200000
.##...###.
.##.####..
.######...
.######...
######....
##.##.....
....#.....
..####....
.#####.##.
.#####.##.
73.540000
...........#...............#..........
...........###..........####..........
...........#####.......####...........
............###############...........
............###############...........
............##############............
.............#############............
............###############...........
...........#################..........
.......#...#################...#......
.......##.##################..##......
........####################.##.......
..........####################........
.........#####..########..#####.......
.......######....#####....######......
......########...#####..########.#....
....#######..#...#####..#..########...
..#########.....#######......#######..
...#######......#######........###....
..####.........#########........###...
...............#########..............
..............##########..............
..............##########..............
...............########...............
...............########...............

数据来源

ふか杯 5th Contest