问题文

尼瓦戈君喜欢堆叠铅笔。今天他决定用以下方法堆叠铅笔。首先，将$N$支铅笔在地板上左右排列成一列。第$i$支铅笔的长度为$L_i$。

然后，将$N-1$支铅笔堆叠在相邻的两支铅笔之间。堆叠在上面的铅笔的长度等于下面两支铅笔中较长的一支。换句话说，设堆叠在上面的铅笔中第$j$支铅笔的长度为$K_j$，则有$K_j=max\\{L_j,L_{j+1}\\}$。

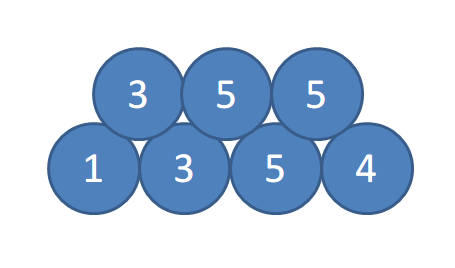
例如，如上图所示的铅笔堆叠方式。这里，圆圈中的数字表示铅笔的长度。

当从上方看堆叠的铅笔时，只能看到堆叠在上面的$N-1$支铅笔的长度，而无法知道底部的$N$支铅笔的长度。在这种情况下，尼瓦戈君想到了一种游戏。你的任务是编写一个能够解答这个游戏的程序。然而，保证存在一组作为底部的铅笔长度的组合。

换句话说，当给定由$N-1$个数字组成的序列$\\{K_j\\}$时，求解满足所有$j$的条件$K_j=max\\{L_j,L_{j+1}\\} (1 ≦ j ≦ N-1)$的铅笔长度序列$\\{L_i\\}$。

输入输出

输入从标准输入读取，具有以下格式。

$N$ $K_1$ $K_2$ … $K_{N-1}$

• 第$1$行，给出作为底部的铅笔数量$N (2 ≦ N ≦ 10^5)$。
• 第$2$行，以空格分隔给出堆叠在上面的铅笔的长度$K_1,...,K_{N-1}$。
• 满足$1 ≦ K_i ≦ 10^9(1 ≦ i ≦ N)$。

输出

以空格分隔，将底部的铅笔长度$L_1,...,L_N$以单行输出。在输出末尾换行。

示例1

4
3 5 5

输出示例1

1 3 5 4

当以长度为$1, 3, 5, 4$的铅笔作为底部，堆叠$3$支铅笔时，堆叠后的铅笔长度分别为$3, 5, 5$。因此，$1, 3, 5, 4$满足条件。

示例2

6
4 8 8 2 5

输出示例2

4 4 8 2 2 5

示例3

5
1 2 3 4

输出示例3

1 1 2 3 4