问题描述

在Niconico镇上，富有的二丸子住着 $N$ 个交叉路口，每个交叉路口都有从 $1$ 到 $N$ 的编号。此外，有 $M$ 条连接两个交叉路口的道路，每条道路都有从 $1$ 到 $M$ 的编号。当通过道路 $i$ 时，可以在 $2^i$ 的时间内从交叉路口 $A_i$ 到交叉路口 $B_i$ 或者从交叉路口 $B_i$ 到交叉路口 $A_i$。

现在，二丸子打算去兜风。他希望将兜风的路线从交叉路口 $1$ 开始，经过所有的 $M$ 条道路至少一次，并返回到交叉路口 $1$。请计算在这样的路线中所需的最小时间。由于答案可能非常大，因此请输出答案对 $1,000,000,007$ 取模的余数。

输入

输入的格式如下，从标准输入中获取。

$N$ $M$ $A_1$ $B_1$ $A_2$ $B_2$ : $A_M$ $B_M$

• 第 $1$ 行包含两个整数，用空格分隔：$N (2 ≦ N ≦ 400,000), M (1 ≦ M ≦ 500,000)$，表示Niconico镇中的交叉路口数为 $N$，道路数为 $M$。
• 接下来的 $M$ 行描述了道路的信息。其中第 $i$ 行包含两个整数 $A_i, B_i (1 ≦ A_i ≦ N, 1 ≦ B_i ≦ N, A_i ≠ B_i)$，表示道路 $i$ 连接着交叉路口 $A_i$ 和交叉路口 $B_i$。不存在连接同一组交叉路口的多条道路。同时，保证任意一对交叉路口都可以通过一些道路到达。

部分分

此问题有部分分。

• 如果满足 $N ≦ 2,525$ 且 $M ≦ 2,525$ 的数据集1，则获得40分。
• 如果对所有测试用例求解正确，则额外获得70分。

输出

输出旅行所需的最短时间，将其除以 $1,000,000,007$ 取模，并输出为一行。末尾要换行。

示例1

4 5
1 2
3 4
2 3
1 3
2 4

示例1输出

70

在这个示例中，Niconico镇具有以下结构。

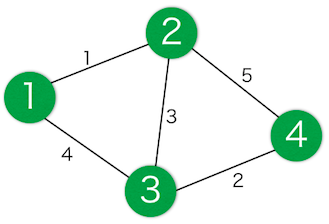
例如，按照交叉路口的顺序 $1,2,3,4,2,3,1$，旅行的时间为 $2^1 + 2^3 + 2^2 + 2^5 + 2^3 + 2^4 = 70$。

示例2

6 10
4 6
4 5
3 6
5 2
3 2
1 2
3 4
6 1
2 4
1 3

示例2输出

2132