問題文

ニワンゴ君が住んでいるニコニコ町には $N$ 個の交差点があり、それぞれの交差点には $1$ から $N$ の番号がついています。また、$2$ つの交差点を結ぶ $M$ 本の道があり、それぞれの道には $1$ から $M$ の番号がついています。道 $i$ を通ると、交差点 $A_i$ から交差点 $B_i$ または 交差点 $B_i$ から交差点 $A_i$ に $2^i$ の時間で行くことができます。

ニワンゴ君は今からドライブに出かけるところです。ドライブの経路は、交差点 $1$ から出発し、$M$ 本全ての道を少なくとも $1$ 回以上通って、交差点 $1$ に戻って来る、というような経路にしたいと思っています。そのような経路をたどってドライブをするときにかかる時間の最小値を求めてください。ただし、答えは非常に大きくなることがあるため、$1,000,000,007$ で割った余りを求めてください。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $M$ $A_1$ $B_1$ $A_2$ $B_2$ : $A_M$ $B_M$

• $1$ 行目には、$2$ つの整数 $N (2 ≦ N ≦ 400,000), M (1 ≦ M ≦ 500,000)$ が空白区切りで与えられる。これは、ニコニコ町にある交差点が $N$ 個、道が $M$ 本であるということを表す。
• $2$ 行目からの $M$ 行では、道の情報が与えられる。このうち $i$ 行目には、$2$ つの整数 $A_i, B_i (1 ≦ A_i ≦ N, 1 ≦ B_i ≦ N, A_i ≠ B_i)$ が与えられる。これは、道 $i$ が 交差点 $A_i$ と交差点 $B_i$ を結んでいることを表す。同じ交差点の組を結ぶ道は $2$ 本以上存在しない。また、どの交差点からどの交差点までも、いくつかの道を通ることによってたどり着けることが保証されている。

部分点

この問題には部分点が設定されている。

• $N ≦ 2,525$ かつ $M ≦ 2,525$ を満たすデータセット $1$ に正解した場合は、$40$ 点が与えられる。
• 全てのテストケースに正解した場合は、上記とは別に $70$ 点が与えられる。

出力

ドライブにかかる時間の最小値を $1,000,000,007$ で割った余りを $1$ 行に出力せよ。出力の末尾に改行を入れること。

入力例1

4 5
1 2
3 4
2 3
1 3
2 4

出力例1

70

この入力例では、ニコニコ町は以下のような構造をしています。

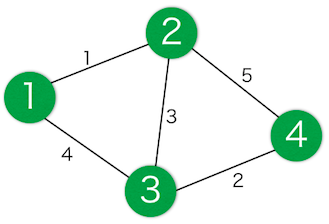
例えば、交差点を $1,2,3,4,2,3,1$ の順でたどるとかかる時間が $2^1 + 2^3 + 2^2 + 2^5 + 2^3 + 2^4 = 70$ となります。

入力例2

6 10
4 6
4 5
3 6
5 2
3 2
1 2
3 4
6 1
2 4
1 3

出力例2

2132