问题描述

甜甜圈店员小姐Naoki Sato负责装甜甜圈盒子。现在，Naoki正在试图将$K$个甜甜圈装入$N$个盒子中。盒子$i (1 \leq i \leq N)$的容积为$C_i$，每个盒子都可以放置一个甜甜圈。

Naoki希望使用所有的盒子。然而，由于盒子的数量多于甜甜圈的数量，她决定通过将盒子嵌套在一起来使用所有的盒子。每个盒子内必须仅放入一个甜甜圈或一个箱子。对于盒子$i$，它可以放入体积比盒子$i$小的箱子。即使嵌套的盒子内部还有其他盒子或者甜甜圈，也会视作1个物体计数。如果将盒子$j$放入盒子$i$，则必须在盒子$i$和盒子$j$之间放入缓冲材料量$C_{i}-C_{j}$。找出所需缓冲材料总量的最小值。

另外，由于Naoki非常笨拙，她可能在装箱过程中压碎盒子。每次Naoki压碎盒子时，请计算此时所需缓冲材料总量的最小值，假设她使用剩余的所有盒子进行装箱。Naoki总共压碎$Q$个盒子，第$i$个被压碎的盒子是$D_i$。

---

输入

输入以以下格式从标准输入中给出。

$N$ $K$

$C_1$ $C_2$ ... $C_N$

$Q$

$D_1$

$D_2$

...

$D_Q$

• 第一行包含两个整数$N (1 \leq N \leq 200,000), K (1 \leq K \leq N)$，以空格分隔。表示开始时有$N$个盒子和$K$个甜甜圈。
• 第二行包含$N$个整数，以空格分隔，表示盒子的容积。其中第$i$个整数$C_i (1 \leq C_i \leq 200,000)$表示盒子$i$的容积。保证对于$p \neq q$，$C_p \neq C_q$。
• 第三行包含一个整数$Q (0 \leq Q \leq N-K)$，表示Naoki压碎的盒子数量。
• 接下来的$Q$行，每行包含一个整数$D_i (1 \leq D_i \leq N)$，表示Naoki压碎的第$i$个盒子是盒子$D_i$。保证对于$p \neq q$，$D_p \neq D_q$。

---

部分分

该问题设有部分分。

• 对于满足$Q = 0$和$K = 2$的数据集1，正确回答将获得15分。
• 对于满足$Q = 0$的数据集2，正确回答将获得额外25分。
• 对于满足$K = 2$的数据集3，正确回答将获得额外30分。

---

输出

输出包含$Q+1$行。第一行输出使用所有盒子进行装箱时所需缓冲材料总量的最小值。接下来的$Q$行中，第$i$行$(1 \leq i \leq Q)$输出Naoki压碎$i$个盒子后使用剩余所有盒子进行装箱时所需缓冲材料总量的最小值。请在输出末尾换行。

---

输入示例1

5 4
1 9 3 7 4
0

输出示例1

1

在此示例中，可以按照如图方式进行装箱，以使所需缓冲材料的总量为1。蓝色区域表示放入缓冲材料的部分。

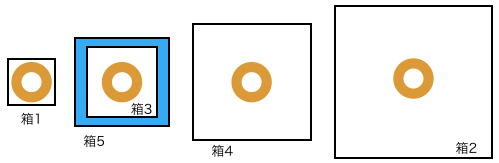
此外，在此示例中，Naoki没有压碎任何盒子。

---

输入示例2

4 2
6 5 10 2
2
3
1

输出示例2

4
1
0

在此示例中，可以按照如图方式进行装箱。蓝色区域表示放入缓冲材料的部分。

---

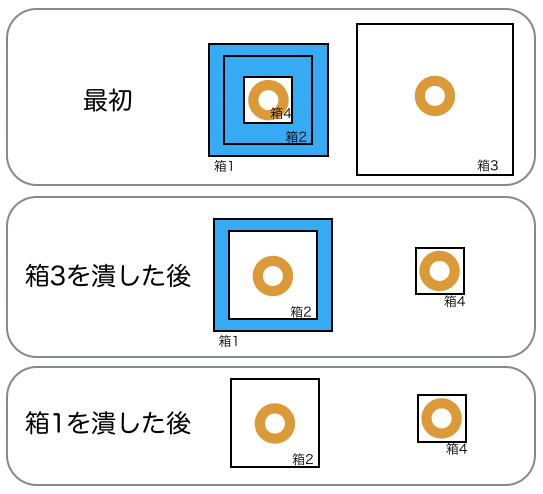
输入示例3

7 3
2 12 3 13 7 17 1
4
4
3
1
6

输出示例3

7
6
6
5
0

---