问题文

问题设置有一些错误。此外，存在一些测试用例满足 R>D 的条件。我将在问题中添加约束 R<D 并进行修正。修正工作完成后，将重新评判。(19:14)

重新评判完成。(19:21)

让我们计算一个甜甜圈的体积。

通过绕着某条直线旋转平面图形可以得到一个立体的体积，该体积可以用以下公式表示：

• “平面图形的面积” × “平面图形的重心所形成的圆的周长”

请计算一个半径为 R 的圆，绕着距离圆心 D 的直线旋转而成的甜甜圈的体积。

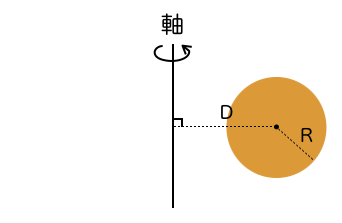
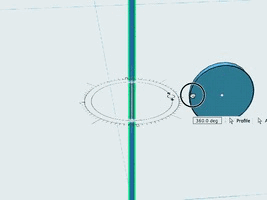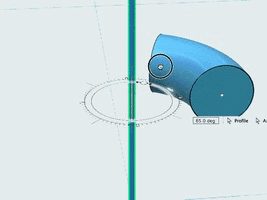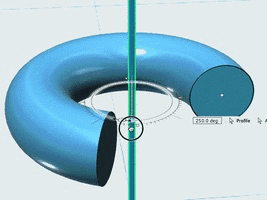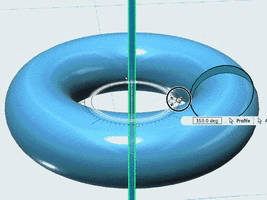
输入

输入从标准输入读取，格式如下：

R D

• 第一行包含两个整数 R (1 ≤ R ≤ 100) 和 D (R < D ≤ 100)，以空格分隔。它们是问题中描述的变量。

输出

将绕着距离圆心 D 的直线旋转而成的半径为 R 的圆的立体体积输出为一行。可以输出任意位小数，但不能包含绝对误差超过 $10^{-2}$ 。在输出的末尾加上换行符。

示例输入 1

3 5

示例输出 1

888.264396

只需要输出半径为 3 的圆，绕着距离圆心为 5 的直线旋转而成的立体体积。

"平面图形的面积" 是 $3^2 × π$，"平面图形的重心所形成的圆的周长" 是 $5 × 2 × π$，所以体积为 $90 × π^2$。

请注意圆的重心是圆心。

示例输入 2

46 96

示例输出 2

4009743.9192393753

之前示例 2 的输入不满足约束条件，因此已被修改。