問題文

問題設定に不備がありました．また，R>Dであるようなテストケースが存在していました．R＜Dという制約を問題に付け加え，テストケースの修正作業を行います．作業が完了次第リジャッジを行います．(19:14)

リジャッジが完了しました．(19:21)

ドーナツの体積を計算してみましょう。

平面図形をある直線を軸に回転させてできる立体の体積は、

• 「平面図形の面積」$\\times$ 「平面図形の重心が描く円の周長」

という式で求めることができます。

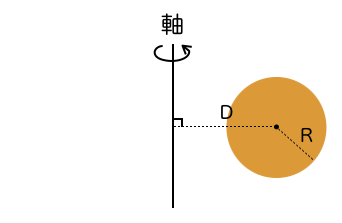
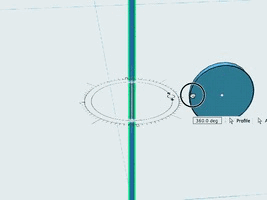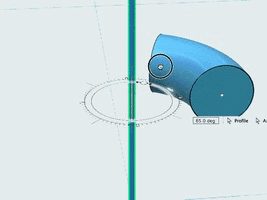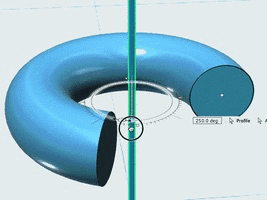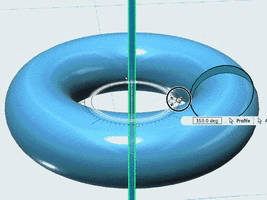
半径 $R$ の円を、円の中心からの距離が $D$ である直線を軸に回転させてできるドーナツ型の立体の体積を計算してください。

入力

入力は以下の形式で標準入力から与えられる。

$R$ $D$

• $1$ 行目には、$2$ つの整数 $R (1 ≦ R ≦ 100),$ D (R ＜ D ≦ 100) が空白区切りで与えられる。これは、問題文中の通りの変数である。

出力

半径が $R$ の円を、円の中心からの距離が $D$ である直線を軸に回転させてできる立体の体積を $1$ 行に出力せよ。小数点以下何桁でも出力してよいが、$10^{−2}$ を超える絶対誤差を含んではならない。出力の末尾に改行を入れること。

入力例1

3 5

出力例1

888.264396

半径が $3$ の円を、円の中心からの距離が $5$ である直線を軸に回転させてできる立体の体積を出力すれば良いです。

「平面図形の面積」は $3^2 \\times π$ で、「平面図形の重心が描く円の周長」は $5 \\times 2 \\times π$ なので、体積は $90 \\times π^2$ となります。

円の重心は中心であることに注意してください。

入力例2

46 96

出力例2

4009743.9192393753

以前のサンプル2の入力は制約を満たしていなかったため，変更されました．