问题文

高桥君是魔方阵的爱好者。

魔方阵是指在一个 $3 \times 3$ 的方阵中放置不同的正整数，使得任意一列（包括对角线）三个整数的和都相等。

高桥君突然想到，是否可以创建一个"乘积版本的魔方阵"，其中三个整数的乘积相等，而不是和相等。

他努力探索后，成功地创建了一个乘积版本的魔方阵，如下图所示：

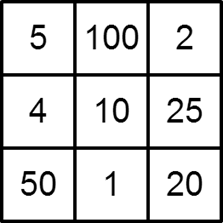
所有列（包括对角线）的乘积都等于 $1000$。

现在，高桥君想知道中间的格子是 $N$ 的乘积版本的魔方阵有多少种可能性。

其中，我们不考虑通过 $90$ 度旋转或左右反转等操作可以相互转换的两个魔方阵是不同的。

请计算中间的格子为 $N$ 的乘积版本的魔方阵的种类数。

---

输入

输入通过标准输入给出，具体格式如下：

$N$

• 第 $1$ 行为乘积版本的魔方阵的中间值 $N$（满足 $1 \leq N \leq 10^{12}$）。

输出

请输出中间的格子为 $N$ 的乘积版本的魔方阵的种类数，输出末尾需要换行。

---

示例输入1

16

示例输出1

1

以下展示的情况中，放置的整数存在重复，因此不是魔方阵。

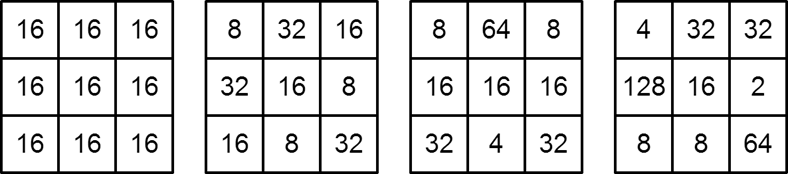
以下展示的情况可以通过旋转或反转等操作变换到相同的情况。

---

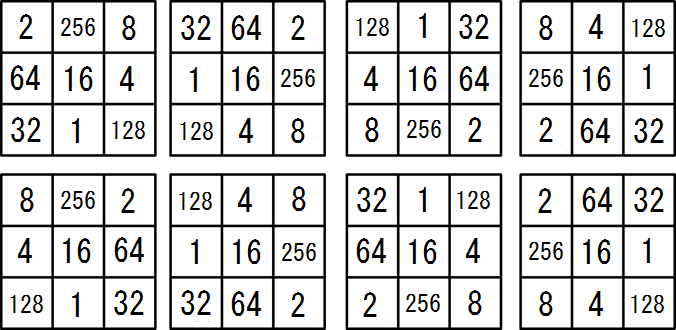
示例输入2

10

示例输出2

1

---

示例输入3

9

示例输出3

0

---

示例输入4

90

示例输出4

29