問題文

$10^{100}$ 個の白いマスが横 $1$ 列に並んでいます。左から $i (1≦i≦10^{100})$ 番目のマスをマス $i$ と呼びます。

また、駒が $N$ 個あり、$i (1≦i≦N)$ 番目の駒を駒 $i$ と呼びます。

さらに、$0$ から $10^{100}$ までの数を数えることのできるカウンタが $1$ つあります。

これらのマスと駒に対し $N$ 回の操作を行います。$i (1≦i≦N)$ 回目の操作は以下のように行います。

1. まず、マス $S_i$ に駒 $i$ を置き、カウンタを $0$ に初期化する。
2. 駒のあるマスの色が白ならそのマスを黒に塗ってカウンタを $1$ 増加させ、駒のあるマスの色が黒なら $1$ つ右のマスに駒を移動させる。
3. $2.$ を繰り返していき、カウンタの値が $C_i$ になったらその時点で操作を終了する。

これらの操作が終わった時点で $N$ 個の駒がそれぞれどのマスにあるかを求めてください。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $S_1$ $C_1$ $S_2$ $C_2$ : $S_N$ $C_N$

• $1$ 行目には、整数 $N (1 ≦ N ≦ 10^5)$ が与えられる。
• $2$ 行目からの $N$ 行には、各操作の情報が与えられる。このうち $i (1 ≦ i ≦ N)$ 行目には、整数 $S_i (1 ≦ S_i ≦ 10^9), C_i (1≦C_i≦10^9)$ が与えられる。これは $i$ 回目の操作のはじめに駒 $i$ を置くマスがマス $S_i$ であり、カウンタが $C_i$ になった時点で操作 $i$ が終了となることを表す。

部分点

この問題には部分点が設定されている。

• 全ての操作が終わった時点での駒のあるマスの番号が全て $10^5$ 以下であるデータセットに正解した場合は、$35$ 点が与えられる。
• $N ≦ 1000$ を満たすデータセットに正解した場合は、上記とは別に $40$ 点が与えられる。
• 追加の制約のないデータセットに正解した場合は、上記とは別に $25$ 点が与えられる。

出力

出力は $N$ 行からなる。このうち $i (1≦i≦N)$ 行目には、全ての操作が終わった時点で駒 $i$ があるマスの番号を表す $1$ つの整数を出力せよ。出力の末尾にも改行を入れること。

入力例1

4
3 3
10 1
4 2
2 4

出力例1

5
10
7
11

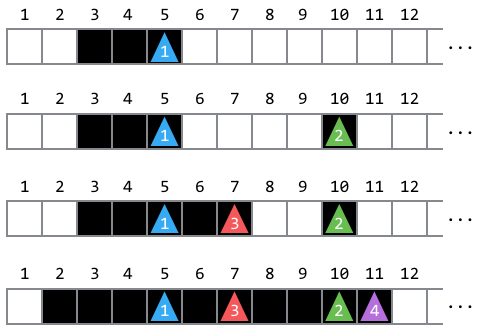
下図は各操作後のマスと駒の状態を表しています。

入力例2

8
2 1
3 1
1 1
5 1
1 1
9 1
8 2
7 9

出力例2

2
3
1
5
4
9
10
18

入力例3

5
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000
1000000000 1000000000

出力例3

1999999999
2999999999
3999999999
4999999999
5999999999

出力が $32$ bit整数型に収まらない場合もあることに注意してください。