问题描述

小明正在玩链接在一起的 $N$ 个气球。气球 $i (1 ≦ i ≦ N)$ 的绳子长度为 $L_i$。小明将气球 $1$ 的绳子抓在手里，然后将气球 $i (2 ≦ i ≦ N)$ 的绳子系在气球 $P_i$ 上。我们称这样连接在一起的气球为“气球树”。

气球树的高度定义为气球树中包含的最高气球的高度。其中，气球 $1$ 的高度为 $L_1$，气球 $i (2 ≦ i ≦ N)$ 的高度为气球 $P_i$ 的高度加上 $L_i$。

小明想要通过解开一些绳子，使得气球树的高度正好等于天花板的高度。他还想知道为了实现这一目标，至少需要解开多少根绳子。当解开气球 $i (2 ≦ i ≦ N)$ 的绳子时，气球 $i$ 以及与其相连的所有气球都会飞走，从气球树中移除。

给定可能的天花板高度的数量 $Q$，请计算每个天花板高度对应的实现目标所需解开的最小绳子数。

输入

输入以以下格式从标准输入中给出。

$N$ $L_1$ $L_2$ ... $L_N$ $P_2$ $P_3$ ... $P_N$ $Q$ $H_1$ $H_2$ : $H_Q$

• 第一行包含一个整数 $N (2 ≦ N ≦ 10^5)$，表示气球的数量。
• 第二行包含 $N$ 个整数，以空格分隔，其中第 $i (1 ≦ i ≦ N)$ 个整数 $L_i (1 ≦ L_i ≦ 10^4)$ 表示气球 $i$ 的绳子长度。
• 第三行包含 $N-1$ 个整数，以空格分隔，其中第 $i (1 ≦ i ≦ N-1)$ 个整数 $P_{i+1} (1 ≦ P_{i+1} ≦ i)$ 表示小明将气球 $i+1$ 的绳子系在气球 $P_i$ 上。
• 第四行包含一个整数 $Q (1 ≦ Q ≦ 10^5)$，表示可能的天花板高度的数量。
• 接下来的 $Q$ 行，每行包含一个整数 $H_i (1 ≦ H_i ≦ 10^9)$，表示天花板的高度。

输出

输出共 $Q$ 行。其中，第 $i (1≦i≦Q)$ 行输出实现气球树高度等于 $H_i$ 所需解开的最小绳子数。如果无法实现高度等于 $H_i$，则输出 $-1$。最后一行也要换行。

示例1

5
1 1 2 2 2
1 2 2 1
2
2
3

输出示例1

3
1

下图分别表示初始的气球树、高度为 $2$ 的气球树、高度为 $3$ 的气球树。红色的叉号表示需要解开的绳子。

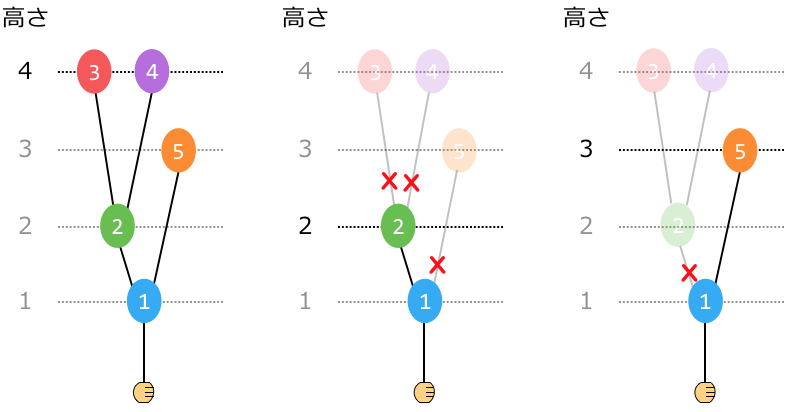
示例2

10
10 5 6 4 2 2 3 1 1 5
1 1 2 2 3 5 7 7 2
5
10
12
15
17
21

输出示例2

2
-1
4
4
0