問題文

りんごさんは、ヒモの付いた $N$ 個の風船を繋げて遊んでいます。風船 $i (1 ≦ i ≦ N)$ のヒモの長さは $L_i$ です。りんごさんは風船 $1$ のヒモを手に持ち、風船 $i (2 ≦ i ≦ N)$ のヒモを風船 $P_i$ にくくりつけました。このようにいくつかの風船が繋がったものを「風船ツリー」と呼ぶことにします。

風船ツリーの高さは、風船ツリーに含まれる風船のうち最も高いものの高さとします。ただし、風船 $1$ の高さは $L_1$ であり、風船 $i (2 ≦ i ≦ N)$ の高さは風船 $P_i$ の高さに $L_i$ を足した値であるとします。

りんごさんは、いくつかのヒモをほどくことで風船ツリーの高さをちょうど天井の高さと同じにしたいと思いました。また、そのためにほどく必要のあるヒモの本数の最小値を知りたいと思いました。風船 $i (2 ≦ i ≦ N)$ のヒモをほどくと、風船 $i$ とそれに繋がった風船が全て飛んで行ってしまい、風船ツリーから取り除かれます。

天井の高さとして考えられる値が $Q$ 個あるので、それぞれについて、風船ツリーの高さをちょうど天井の高さと同じにするためほどく必要のあるヒモの本数の最小値を求めてください。

入力

入力は以下の形式で標準入力から与えられる。

$N$ $L_1$ $L_2$ ... $L_N$ $P_2$ $P_3$ ... $P_N$ $Q$ $H_1$ $H_2$ : $H_Q$

• $1$ 行目には、風船の個数を表す整数 $N (2 ≦ N ≦ 10^5)$ が与えられる。
• $2$ 行目には、$N$ 個の整数が空白区切りで与えられる。このうち $i (1 ≦ i ≦ N)$ 番目の整数 $L_i (1 ≦ L_i ≦ 10^4)$ は、風船 $i$ のヒモの長さを表す。
• $3$ 行目には、$N-1$ 個の整数が空白区切りで与えられる。このうち $i (1 ≦ i ≦ N-1)$ 番目の整数 $P_{i+1} (1 ≦ P_{i+1} ≦ i)$ は、りんごさんが風船 $i+1$ のヒモを風船 $P_i$ にくくりつけたことを表す。
• $4$ 行目には、天井の高さとして考えられる値の個数を表す整数 $Q (1 ≦ Q ≦ 10^5)$ が与えられる。
• $5$ 行目からの $Q$ 行のうち $i (1 ≦ i ≦ Q)$ 行目には、天井の高さを表す整数 $H_i (1 ≦ H_i ≦ 10^9)$ が与えられる。

出力

出力は $Q$ 行からなる。このうち $i (1≦i≦Q)$ 行目には、風船ツリーの高さをちょうど $H_i$ にするためほどく必要のあるヒモの本数の最小値を出力せよ。ただし、ちょうど $H_i$ にすることができない場合は、代わりに $\-1$ を出力せよ。出力の末尾にも改行を入れること。

入力例1

5
1 1 2 2 2
1 2 2 1
2
2
3

出力例1

3
1

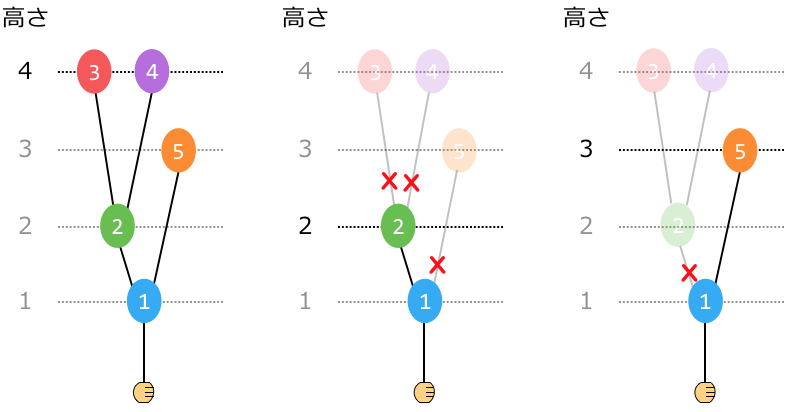
下図はそれぞれ、最初の風船ツリー、高さを $2$ にした風船ツリー、高さを $3$ にした風船ツリーの様子を表しています。赤い×印は、ヒモをほどく箇所を表しています。

入力例2

10
10 5 6 4 2 2 3 1 1 5
1 1 2 2 3 5 7 7 2
5
10
12
15
17
21

出力例2

2
-1
4
4
0