因为此题是道非常残忍的题，可以的话我认为你应该先开心地做其他题，如果其他题做完了还有时间的话，就以此题为消遣吧（以上为题目名称）

题目背景

如果你想AK这场比赛（お誕生日コンテスト），你可以尝试挑战这道题。从准备比赛的阶段开始，我就很担心我是否可以出这样的题目，但我还是决定冒一次险，因为这是一场具有挑战性的比赛。

题目描述

啊~累死我了！这样一来比赛的准备终于完成了！

其实，在我考虑最后一题的时候关于这场比赛的讨论就开始了。

其实与其说是最终问题，不如说是boss问题←

为了不辜负大家的期待，我很愿意挑战出这道最难题2333。

以下是出题者们对大家说的话：

きゅうり：“感谢大家参加比赛，有些问题确实很‘ 可恶 ’，但也不要在意哦！”

JAPLJ：“啊，谢谢大家！这些问题的确很有趣吧？”

KyuR1：“虽说解出了题会很高兴，但是惩罚(?)也有很多啊~”

じゃっぷる：“感谢大家来做题。说实话，这个题面几乎是复制粘贴来的。”

kyuridenamida：“……谢谢大家。”

最后，

きゅうり、JAPLJ、KyuR1、じゃっぷる、kyuridenamida、高桥：“感谢大家的参与！”

（完）

きゅうり、JAPLJ、KyuR1、じゃっぷる、kyuridenamida：“诶？为啥有高桥君啊？重来一遍，感谢大家的参与！”

真的真的结束了。

任务

给出一个式子，由一位数整数，括弧，四则运算符号(加减乘除)组成，请输出计算结果。（译者注：请不要忙着打，先把后面看完。）

输入

$$t$$ $$W \space H$$ $$B_1$$ $$B_2$$ $$\dots$$ $$B_H$$

其中， $t$ 是非负整数，表示此为第 $t$ 组数据。 $W$ 和 $H$ 都是正整数，分别表示输入的图像的横长和纵长。

对于任意 $B_i(1 \leq i \leq H)$ ，都是由'.'和'#'组成的长为 $W$ 的字符串。它的第 $j$ 个字符 $(1 \leq j \leq W)$ 表示图像从上数第 $i$ 行，从左数第 $j$ 列的像素。如果此字符为'.'，则表示该像素为白色；如果此字符为'#'，则表示该像素为黑色。

输出

$$A$$

$A$ 表示输入图像中黑色像素组成的表达式的计算结果。

数据范围

• 对于所有输入数据，满足 $H=65$ 且 $1 \leq W \leq 9000$ 。

所有输入数据按以下步骤生成。

• 开始时给出长度小于等于 $L$ 的包含一位数整数，括弧，四则运算符号的表达式，计算结果和运算过程中得出的数都在 $32$ 位有符号整数型的范围内（数据不一定是随机的）。另外，除法运算只保留整数。也就是说，舍弃代数意义上商的小数部分（比如， $-7/3=-2$ ）。但是，不存在像 $-5$ 这样的负数和像 $-(2+3)$ , $+1$ 这样的最前面带符号的项。
• 表达式中所含的每个字符对应的图像生成方法如下：
• 字体使用Courier Prime，字体大小为 $64$ ，生成描绘该字体粗体字的二进制图像。像这样生成的图像，与由它转换而来的由'.'和'#'组成的文本，都能够在此页下方的提示中进行下载。
• 生成倍率 $M(M \leq 1)$ ，将图片整个扩大成原来的 $M$ 倍（实际上就是在缩小）。
• 生成纵向倍率 $M_h(M_h \leq 1)$ 和横向倍率 $M_w(M_w \leq 1)$ ，将图片纵向上变为原来的 $M_h$ 倍，横向上变为原来的 $M_w$ 倍。
• 生成角度 $R$ ，将整个图片旋转 $R$ 度。
• 生成两个参数 $S_x$ 和 $S_y$ ，根据这个参数来使图像失真。具体来说，将坐标为 $(x,y)$ 的像素移动到 $(x+S_yy,S_xx+y)$ 。
• 将每个字符对应的图像横向连接起来组成一个新的图像，此时：
• 对于横向的位置，对于任意相邻的字符，它们之间会有 $10$ 个像素的空白。
• 对于纵向的位置，对于整个图像在进行扩大缩小，旋转，失真的操作之前图像的大小，是在合适的范围内随机决定的。
• 最后为概率 $P$ ，使每个像素都有 $P$ 的概率会黑白反转（因此你可能需要降噪）。

这里表达式长度上限 $L$ 和noise的概率 $P$ 是对整幅图适用的，而倍率 $M,M_h,M_w$ ,角度 $R$ ,失真参数 $S_x,S_y$ 是对于表达式中每个字符互相独立的。

数据范围

这个问题的数据有 $140$ 组，这些数据从 $0$ 开始编号。这就对应着输入数据中 $t$ 的值。另外，以下 $x∈[a,b]$ 这样的记法表示“ $x$ 是大于等于 $a$ ，小于等于 $b$ 的任一实数”。

• 对于 $0 \leq t < 30$ 的输入数据：
• $L=3$
• $M∈[0.9,1]$
• $M_h∈[0.9,1],M_w∈[0.9,1]$
• $R∈[-2,2]$
• $S_x=0,S_y=0$
• $P=0$
• 对于 $30 \leq t < 90$ 的输入数据：
• $L=50$
• $M∈[0.9,1]$
• $M_h∈[0.9,1],M_w∈[0.9,1]$
• $R∈[-10,10]$
• $S_x∈[-0.1,0.1],S_y∈[-0.1,0.1]$
• $P=0.05$
• 对于 $90 \leq t < 140$ 的输入数据：
• $L=200$
• $M∈[0.9,1]$
• $M_h∈[0.9,1],M_w∈[0.9,1]$
• $R∈[-15,15]$
• $S_x∈[-0.1,0.1],S_y∈[-0.1,0.1]$
• $P=0.05$

分数按以下方式进行计算：

• 对于 $0 \leq t < 55$ 的数据，每组数据 $2$ 分。
• 对于 $55 \leq t < 90$ 的数据，每组数据 $4$ 分。
• 对于 $90 \leq t < 140$ 的数据，每组数据 $5$ 分。

另外，对于 $30 \leq t < 50$ 的数据，输入文件和可视化图片(PNG)可以进行下载。此处

输入输出样例

举例来说，考虑将以下图像作为输入的情况。

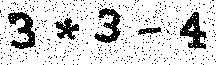
此图对应的输入数据 （由于原数据尺寸太大不便观察，所以此链接中的数据已经经过缩放处理以便理解。此链接中的数据组数编号‘999’也是假的。）

对此式 $(3×3-4)$ 进行计算得出结果：

5

提示

字体数据

$'\space0123456789()+-*/\space'$ 这十六个字符的图像和文字形式的字体数据(zip)可以在此链接处下载。将此zip文件解压可以得到两个文件夹：txt/和png/。这两个文件夹中包含了文字形式和图像(PNG)形式的字体数据。

文字形式的数据省略了 $t$ ，只给出 $W$ 和 $H$ 。

文本嵌入提示

将以上所述的标准字体嵌入到程序中的文本可以在 此处 下载。你也可以对其进行一些加工。

** 注意： ** 光这个嵌入文本就占了约 $44,000bites$ 。AtCoder允许提交的最长代码长度为** UTF-8标准的 $60,000$ 字符以下 **，所以写程序的时候请务必注意程序的长度。

我们的努力

标程能够通过所有测试数据，以及用和生成测试数据一样的方法生成的另外大约 $200$ 组数据。（我们也尽梨了）

感谢@ミク 提供的翻译