问题描述

我们有一个 $H \times W$ 的网格板。网格中的每个方格都被涂成黑色或白色。如果第 $i$ 行从上往下数的第 $j$ 列从左往右数的字符是 #，则表示该方格是黑色；如果该字符是 .，则表示该方格是白色。

Snuke 可以对网格进行以下操作，可以任意多次执行：

• 选择一行或一列，并翻转该行或该列中所有方格的颜色（即，黑色变为白色，白色变为黑色）。

然后，Snuke 沿着网格线绘制一个矩形。在这里，矩形内的所有方格都必须被涂成黑色。

找出当操作被优化执行时，Snuke 的矩形的最大可能面积。

约束条件

• $2 \leq H \leq 2000$
• $2 \leq W \leq 2000$
• $|S_i| = W$
• $S_i$ 由 # 和 . 组成。

输入格式

输入通过标准输入给出，格式如下：

$H$ $W$ $S_1$ $S_2$ $:$ $S_H$

输出格式

打印 Snuke 矩形的最大可能面积。

示例输入1

3 3
..#
##.
.#.

示例输出1

6

如果将从上往下的第一行和从左往右的第三列翻转，就可以得到一个 $2 \times 3$ 的矩形，如下图所示：

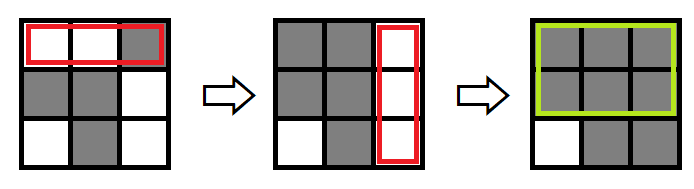
示例输入2

4 4
....
....
....
....

示例输出2

16

示例输入3

10 8
##...#.#
##...#.#
..###.#.
#.##.#.#
.#..#.#.
..##.#.#
##.#.#..
...#.#..
###.#.##
###..###

示例输出3

27