题目描述

在一个二维平面上，有$m$条与$x$轴平行的直线和$n$条与$y$轴平行的直线。其中，与$x$轴平行的第$i$条直线表示为$y = y_i$；与$y$轴平行的第$i$条直线表示为$x = x_i$。

对于由这些直线形成的每一个矩形，找到其面积，并以$10^9+7$为模打印总面积。

换句话说，对于每一组满足条件的四元组$(i, j, k, l)$，其中$1\leq i < j \leq n$且$1\leq k < l \leq m$，找到由直线$x=x_i$、$x=x_j$、$y=y_k$和$y=y_l$形成的矩形的面积，并打印这些面积之和对$10^9+7$取模的结果。

约束条件

• $2 \leq n,m \leq 10^5$
• $-10^9 \leq x_1 < ... < x_n \leq 10^9$
• $-10^9 \leq y_1 < ... < y_m \leq 10^9$
• $x_i$和$y_i$都是整数。

输入和输出

输入按以下格式从标准输入给出：

$n$ $m$ $x_1$ $x_2$ $...$ $x_n$ $y_1$ $y_2$ $...$ $y_m$

输出打印矩形的总面积对$10^9+7$取模的结果。

示例

以下示例中，输入为$n=3$，$m=3$，$x_1=1$，$x_2=3$，$x_3=4$，$y_1=1$，$y_2=3$，$y_3=6$。

输入

3 3
1 3 4
1 3 6

输出

60

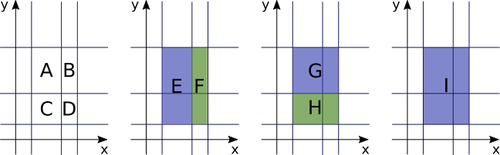
下图说明了这个输入：

图中所示的九个矩形A、B、......、I的总面积为$60$。

以下示例中，输入为$n=6$，$m=5$，$x_1=-790013317$，$x_2=-192321079$，$x_3=95834122$，$x_4=418379342$，$x_5=586260100$，$x_6=802780784$，$y_1=-253230108$，$y_2=193944314$，$y_3=363756450$，$y_4=712662868$，$y_5=735867677$。

输入

6 5
-790013317 -192321079 95834122 418379342 586260100 802780784
-253230108 193944314 363756450 712662868 735867677

输出

835067060