题目描述

AtCoDeer 是一只鹿，他有 $N$ 块正方形瓷砖。这些瓷砖的编号从 $1$ 到 $N$，每块瓷砖上都写着相应的编号。此外，每个瓷砖的四个角落都涂成了 $0$ 到 $999$ 之间的 $1000$ 种颜色之一，用整数 $0$ 到 $999$ 表示。当从瓷砖上写的编号所在的方向看时，编号为 $i$ 的瓷砖的左上角、右上角、右下角和左下角被涂成颜色 $C_{i,0}, C_{i,1}, C_{i,2}$ 和 $C_{i,3}$（参见图 $1$）。

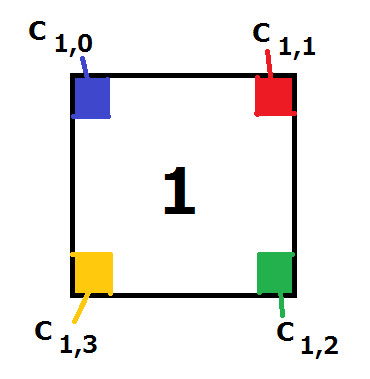
图 $1$: 瓷砖颜色与输入的对应关系

AtCoDeer 正在使用这些瓷砖组装一个立方体，并需满足以下条件：

• 每块瓷砖的编号处于立方体的外部。
• 对于立方体的每个顶点，构成它的三个瓷砖的角落颜色必须完全相同。

请帮助他找出在满足条件的情况下可以组装的不同立方体的数量。由于每个瓷砖上都写有编号，如果使用的瓷砖集合不同或者瓷砖使用的方向不同，即使颜色的排列相同，也会认为是不同的立方体。（每块瓷砖可以按照 $90°$ 的旋转获得四个方向。）只有在三维空间中旋转一个立方体能够精确地获得另一个立方体（包括瓷砖的方向）时，才认为两个立方体是相同的。

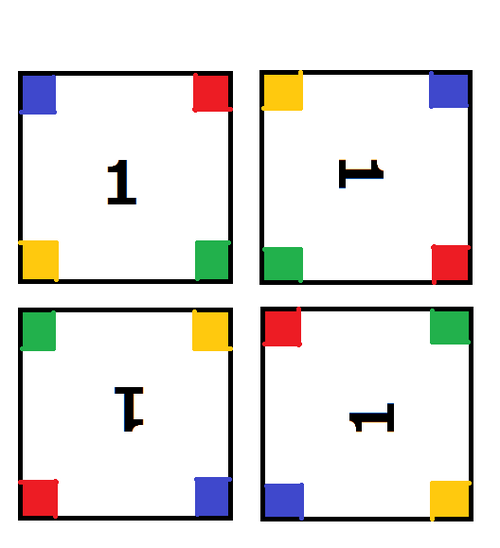
图 $2$: 一个瓷砖的四个方向

约束条件

• $6≦N≦400$
• $0≦C_{i,j}≦999 (1≦i≦N , 0≦j≦3)$

输入

输入从标准输入读入，输入格式如下：

$N$ $C_{1,0}$ $C_{1,1}$ $C_{1,2}$ $C_{1,3}$ $C_{2,0}$ $C_{2,1}$ $C_{2,2}$ $C_{2,3}$ $:$ $C_{N,0}$ $C_{N,1}$ $C_{N,2}$ $C_{N,3}$

输出

输出满足条件的不同立方体的数量。

示例输入1

6
0 1 2 3
0 4 6 1
1 6 7 2
2 7 5 3
6 4 5 7
4 0 3 5

示例输出1

1

可以组装以下立方体。

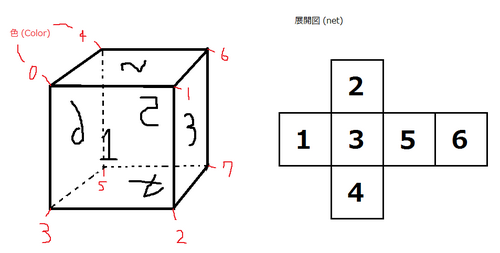
示例输入2

8
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 0
1 1 1 1

示例输出2

144

示例输入3

6
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0

示例输出3

122880