问题

高桥君在旅行中参观了一棵奇怪的完全二叉树，它被称为"Swap-Tree"。

"Swap-Tree"是一棵高度为$N+1$、叶子节点数量为$2^N$的完全二叉树。叶子节点上按照从左到右的顺序标有数字$1,2,3,...,2^N$。

此外，对于非叶子节点，定义了一个属性叫做"位置"，在第$i$层从上到下的第$j$个位置$(1≤i≤N, 1≤j≤2^{i-1})$，其位置编号为$2^{i-1} + (j-1)$。

另外还定义了一个操作${\\rm swap}(x)$，这个操作的作用是找到位置为$x$的节点，并交换其左右子树。

"Swap-Tree"可以处理以下两种类型的查询：

类型1：给定$k(1≤k≤2^N)$，找出从左到右第$k$个叶子节点上的数字。

类型2：给定$a, b(1≤a≤b≤2^N - 1)$，按照顺序执行${\\rm swap}(a), {\\rm swap}(a+1), {\\rm swap}(a+2), ..., {\\rm swap}(b)$这些操作。

高桥君回到家后，也想自己制作一棵"Swap-Tree"，但是发现很难，所以决定由你来制作。

具体来说，给定$N$和$Q$个查询，请你构建一棵能够处理这些查询的"Swap-Tree"。

输入

输入通过标准输入给出，格式如下：

$N$ $Q$ $t_1$ $a_1$ $b_1$ $t_2$ $a_2$ $b_2$ : $t_Q$ $a_Q$ $b_Q$

• 第$1$行为两个整数$N(1≤N≤17)$和$Q(1≤Q≤200,000)$，以空格分隔。
• 接下来的$Q$行中，描述了$Q$个查询。其中第$i$行包含三个整数$t_i$、$a_i$、$b_i$，以空格分隔。
• 当$t_i = 1$时，表示为类型1的查询，其中$a_i$对应问题描述中的$k$，而$b_i$必定为$0$。
• 当$t_i = 2$时，表示为类型2的查询，其中$a_i$和$b_i$分别对应问题描述中的$a$和$b$。

输出

对于每一个类型1的查询，输出查询结果。每次输出后换行。

示例1

3 10
2 5 5
1 1 0
1 2 0
1 3 0
1 4 0
2 1 3
1 2 0
1 3 0
1 5 0
1 6 0

输出示例1

1
2
4
3
8
5
4
3

在这个示例中，有两个类型2的查询。

第一个类型2的查询之后，"Swap-Tree"的结构如下图所示：

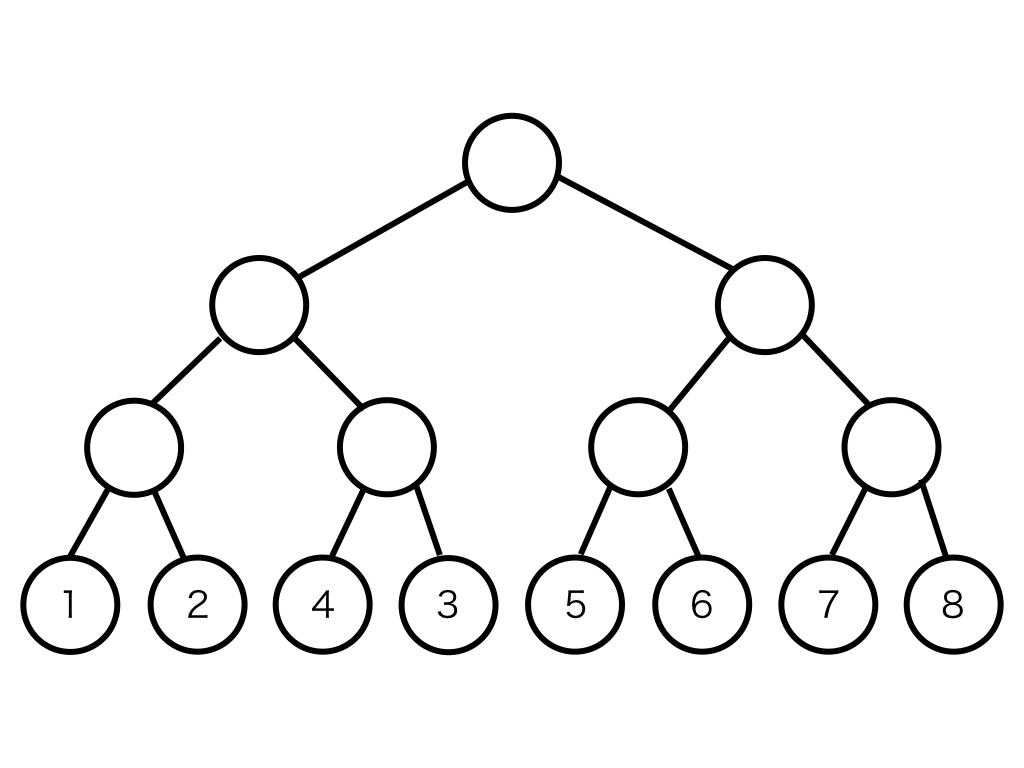
第二个类型2的查询之后，"Swap-Tree"的结构如下图所示：