#arc047d. [arc047_d]ナナメクエリ
[arc047_d]ナナメクエリ
问题文
有一个 行 列的方格纸。
我们将方格纸左上角的格子称为 ,下移 格,右移 格后的格子称为 。即左上角的格子是 ,右下角的格子是 。
一开始,每个格子上都写着数字 。
现在我们要进行 次查询操作。查询操作有 种,如下所示:
1 A B C:将满足 的格子 上的数字加上 。保证 ,。2 A B C:将满足 的格子 上的数字加上 。保证 ,。3 A B C D:找出满足 且 的所有格子中最大的数字 ,并统计在这个范围内数字等于 的格子的数量。保证 ,。
请编写程序按顺序处理这些查询操作。
输入
输入从标准输入中读取,具体格式如下:
:
- 第 行包含两个用空格分隔的整数,表示方格纸的大小 和查询操作的数量 。
- 接下来的 行中,第 行表示第 个查询操作。查询的格式如问题文中所述。
- 保证至少有 个第 种查询。
部分分
本问题设置了部分分。
- 如果能正确处理满足 的数据集,将得到 分。
- 如果能正确处理满足 的数据集,将额外得到 分。总共可以得到 分。
- 如果能正确处理满足 的数据集,将额外得到 分。总共可以得到 分。
输出
输出行数与第 种查询的数量相等。第 行输出第 个第 种查询的答案。设范围内最大值为 ,范围内等于 的格子数量为 ,则按顺序输出 和 ,以空格分隔。最后换行。
输入示例1
4 4
1 1 4 2
3 0 1 2 3
2 -2 1 3
3 0 3 1 3
输出示例1
2 4
5 7
处理完第 个查询后的方格纸如下所示:
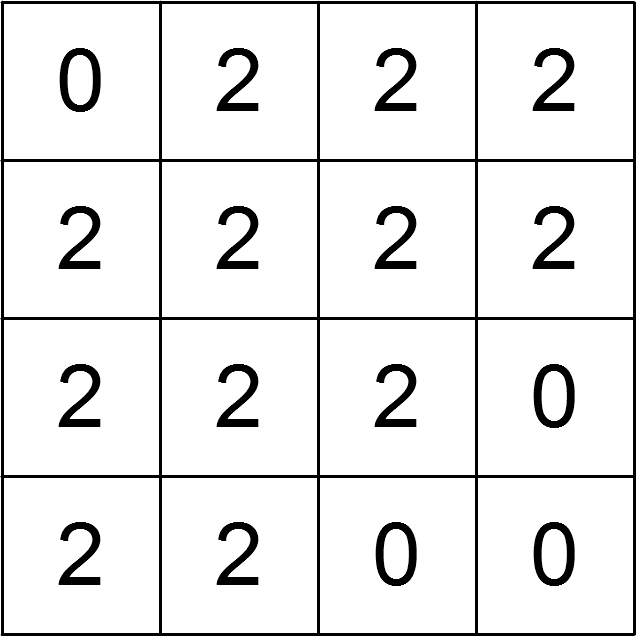
第 个查询的范围如下所示:
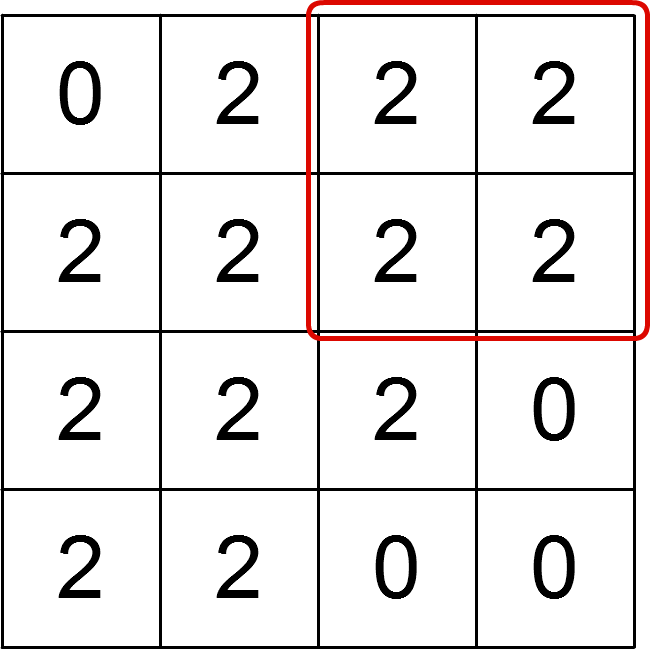
因此最大值为 ,数量为 。
处理完第 个查询后的方格纸如下所示:

第 个查询的范围如下所示:

因此最大值为 ,数量为 。
输入示例2
50 20
2 5 40 6
1 69 94 5
3 8 39 31 32
2 -29 -21 -10
2 20 43 3
2 -37 36 -10
2 -18 45 5
2 30 39 -2
3 0 1 19 33
3 27 47 0 43
3 0 1 28 39
1 90 97 0
2 -46 31 7
1 81 81 4
1 11 54 3
3 10 29 26 30
1 39 45 3
1 70 97 -4
3 24 46 14 34
3 1 18 48 48
输出示例2
11 5
-5 1
14 8
0 3
5 82
16 2
10 5
