问题说明

多桥君非常喜欢桥。因此，他喜欢称为树的图，其中所有边都是“桥”（图论术语）。此外，多桥君最近在学校学习了异或运算（XOR）。因此，他正在思考以下问题。

给定一个由 $N$ 个顶点和 $N-1$ 条边组成的连通无向图，即树。每个顶点都被称为顶点1、2、...、N。每条边上都分配了非负整数的成本。

给定一个整数 $X$，请计算满足以下条件的顶点 $a$ 和顶点 $b$ 的数量：它们在连接点上有一条简单路径（在树中只存在一条）且该路径上的边的费用的异或和等于 $X$（$1 \leq a < b \leq N$）。其中异或和指的是，当有一些整数 $A_1,A_2,...$ 时，它们的二进制表示的每位进行异或运算得到的值。例如，$1$ XOR $2$ XOR $5$ 等于 $6$。

你的任务是代表多桥君解决这个问题。

输入

从标准输入读入输入数据，输入格式如下所示：

$N$ $X$ $x_1$ $y_1$ $c_1$ $x_2$ $y_2$ $c_2$ : $x_{N-1}$ $y_{N-1}$ $c_{N-1}$

• 第 1 行包含两个整数，$N$ 表示图中的顶点数 $(1 \leq N \leq 100,000)$，$X$ 是问题描述中的整数 $(0 \leq X \leq 10^9)$。
• 接下来的 $N-1$ 行给出了图中 $N-1$ 条边的信息。其中第 $i$ 行包含连接第 $i$ 条边的两个顶点 $x_i$ 和 $y_i$ $(1 \leq x_i, y_i \leq N)$，以及该边的成本 $c_i$ $(0 \leq c_i \leq 10^9)$。
• 给定的图保证是连通的。

输出

输出满足问题描述中要求的答案。

输入示例1

6 7
1 2 5
2 3 3
3 4 6
2 5 2
5 6 7

输出示例1

3

当 $(a,b)=(1,5)$，$(4,5)$，$(5,6)$ 时，路径上的边的费用的异或和为 $7$（二进制表示为 $111$），所以答案为 $3$。

对于这个输入示例，图如下所示，显示了每条边的十进制和二进制表示：

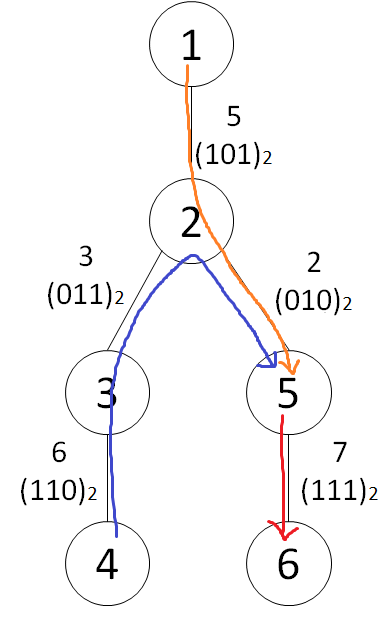
输入示例2

6 3
1 2 1
2 3 3
3 4 2
4 5 3
4 6 1

输出示例2

4

输入示例3

10 1
9 10 1
6 10 1
5 2 1
8 6 1
4 5 1
7 6 0
3 8 0
3 1 1
8 2 0

输出示例3

25