问题描述

高桥君非常喜欢最短路径算法。他每天都在实现和玩各种最短路径算法。但是，高桥君由于求解最短路径的次数太多，已经对求解最短路径感到厌倦了。

因此，高桥君决定统计某个顶点到其他顶点的最短距离为特定值的顶点数量为$N$，并且所有边的长度均为1的无向简单图的数量。

更准确地说，高桥君按照顶点$1,2,...,N$依次编号的方式给定图的顶点，其中不存在多条连接同一顶点之间，且每条边的两个端点顶点不同的图。他要计算满足对任意$i$，顶点$1$和顶点$i$之间的路径上存在的边的最小个数为$A_i$的图的总数。

给定整数$N$和$A_1,...,A_N$，请计算满足条件的图的数量除以$10^9+7$所得的余数。

---

输入

输入从标准输入读取，具有以下格式。

$N$ $A_1 A_2 ... A_N$

• 第$1$行包含图的顶点数$N(1 ≦ N ≦ 10^5)$。
• 第$2$行包含以空格分隔的整数序列$A_1,...,A_N(0 ≦ A_1,...,A_N ≦ N-1)$，表示从顶点$1$到顶点$i$的最短距离。

输出

输出满足条件的图的数量除以$10^9+7$所得的余数。

请在输出末尾添加换行符。(已修正于21:40)

---

示例1

4
0 1 1 2

输出示例1

6

下图中的$6$种图满足条件。

---

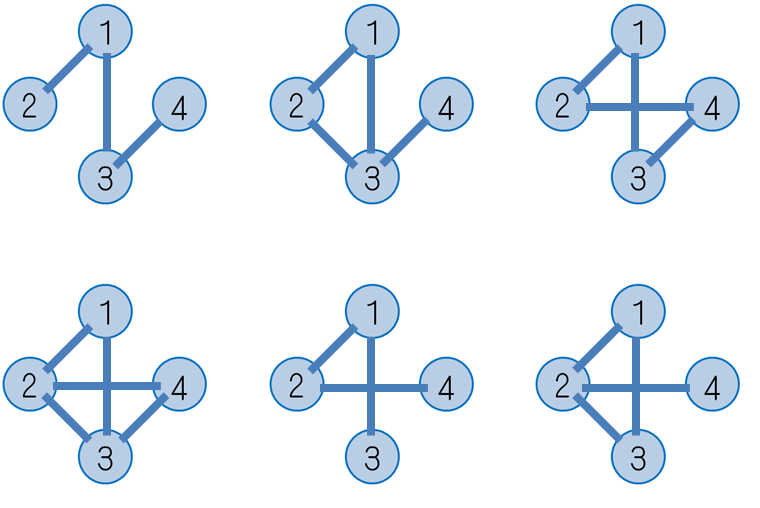
示例2

4
0 1 2 0

输出示例2

0

由于所有边的长度为$1$，因此不存在顶点$1$和顶点$4$之间距离为$0$的图。

---

示例3

3
1 1 2

输出示例3

0

顶点$1$到顶点$1$的距离不可能为$1$。

---

示例4

17
0 1 1 2 2 4 3 2 4 5 3 3 2 1 5 4 2

输出示例4

855391686

---