问题描述

对于非负整数 $L$，级别为$L$的Sierpinski gasket是指以下形状：

• 级别为0的Sierpinski gasket是一个正三角形。
• 级别为$i$（$i≥1$）的Sierpinski gasket是通过对级别为$i-1$的Sierpinski gasket中的每个包含的$3i-1$个正三角形进行以下操作得到的： （操作）连接每个正三角形的边的中点，并在中心创建一个小正三角形。从图形中去除这个小正三角形（结果是原始正三角形被分割成三个小正三角形）。

下面显示了级别为$0, 1, 2, 3, 4$的Sierpinski gasket的示意图。

给定正整数$L$。考虑级别$L$的Sierpinski gasket中所有包含的$3L$个正三角形的边。求由这些线段组成的简单多边形（非自交多边形）的数量，将其除以$1,000,000,007$并求余数。即使它们是相似的多边形，如果位置不同也要区分开来。

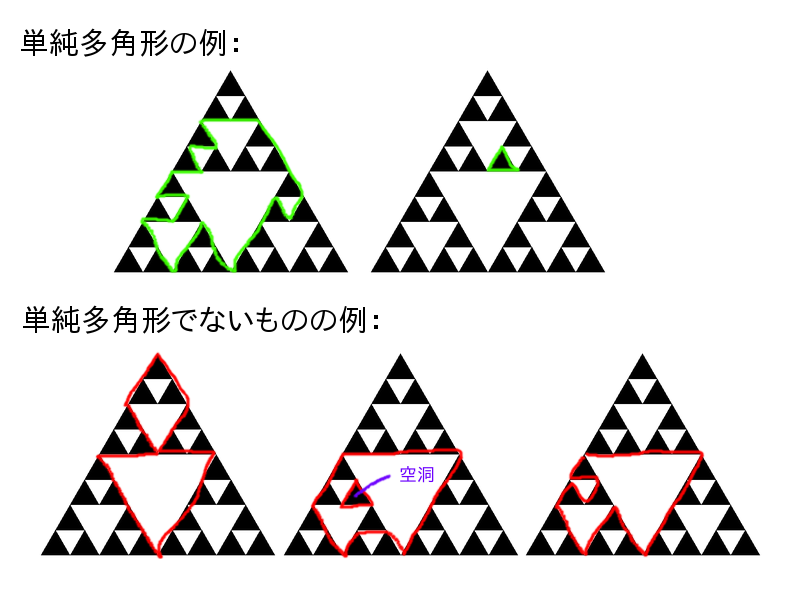
下面展示了应计算的多边形和不应计算的多边形的例子。

---

输入

输入通过标准输入给出，格式如下：

$L$

• 第1行包含整数$L$（$1 ≤ L ≤ 105$）。

---

输出

输出计算出的多边形的数量，并将其除以$1,000,000,007$并求余数，然后换行。

---

输入示例1

1

输出示例1

11

存在以下11个简单多边形。

---

输入示例2

2

输出示例2

1033

---

输入示例3

3

输出示例3

30304092

---

输入示例4

123

输出示例4

853343829