#arc035d. [arc035_d]高橋くんとマラソンコース
[arc035_d]高橋くんとマラソンコース
问题文
高桥君是马拉松比赛的主办者,他正在制定下一届马拉松比赛的计划。他所在的城市有东西和南北两个方向各有 条道路,在南北方向上,从西边延伸的第 条道路和在东西方向上,从南边延伸的第 条道路交叉的交叉点表示为 。
为了简化马拉松赛道的建设,道路只能往东或往北走。高桥君确定了 个检查点 作为参与者计时的位置。
在高桥君的城市中,由于参与者希望每个人都选择不同的路径参加马拉松比赛,因此不同路径的数量很重要。根据计时需求,当设置了从检查点 到检查点 的马拉松赛道时,参与者必须经过所有满足 的检查点 。
因此,高桥君需要回答以下 个查询:
- 将第 个检查点的位置更改为 。
- 判断从检查点 到检查点 的不同路径总数和从检查点 到检查点 的不同路径总数哪个更大。 注意,保证路径数量较多的一方至少是路径数量较少的一方的两倍以上。
请编写一个程序来帮助高桥君。
输入
输入以以下格式从标准输入中给出。
: :
- 第行为表示检查点数量的整数 。
- 接下来的行,每行表示检查点的位置的整数 ,以空格分隔。
- 第行为表示查询数量的整数 。
- 第行到第行,每行表示一个查询。 表示第个查询的类型。
- 当 时,该行有三个整数 ,以空格分隔。
- 当 时,该行有四个整数 $l_{1j}, r_{1j}, l_{2j}, r_{2j} (1 ≦ l_{1j} < r_{1j} ≦ N, 1 ≦ l_{2j} < r_{2j} ≦ N )$,以空格分隔。
- 对于任意 ,确保从检查点 到检查点 的路径始终存在一条(即使通过查询改变了检查点的位置)。并且,检查点的位置不会重叠。
部分分
此问题有部分得分。
- 在30个测试案例中,满足 。
输出
对于类型为 的查询,按给定的查询顺序逐行输出答案。如果从检查点 到 检查点 的路径较多,则输出 FIRST;如果从检查点 到检查点 的路径较多,则输出 SECOND。
不要忘记输出末尾的换行符。
输入示例1
4
1 1
2 5
4 5
5 6
4
2 1 3 3 4
2 1 3 1 4
1 2 2 2
2 2 3 3 4
输出示例1
FIRST
SECOND
FIRST
对于第 个查询,从检查点 到检查点 的路径数为 。
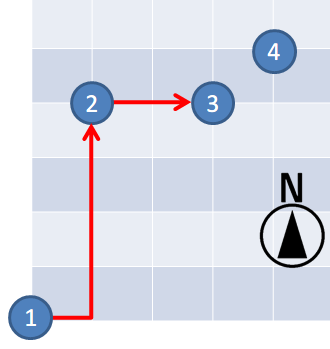
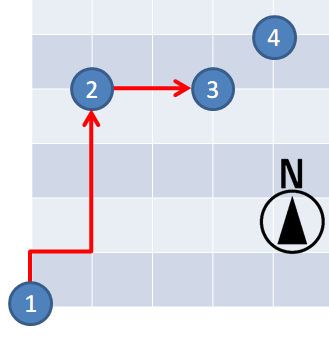
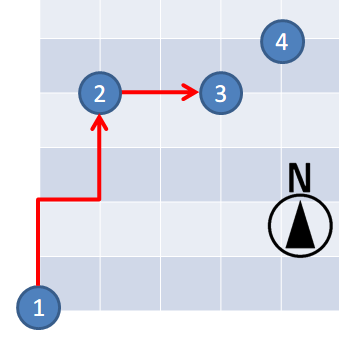
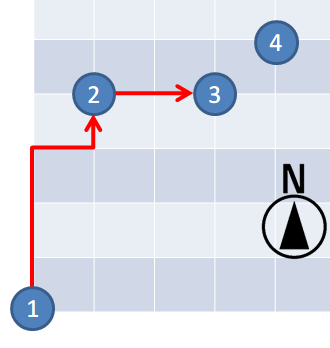
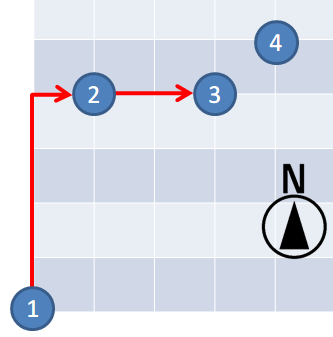
从检查点 到检查点 的路径数为 。
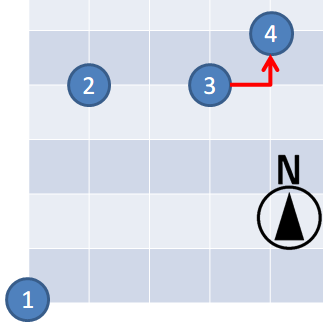
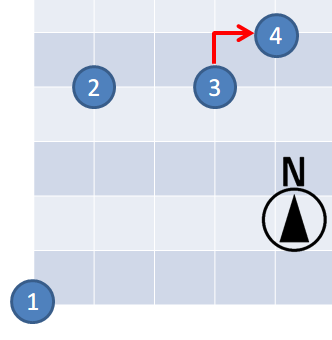
因此,输出 FIRST。
对于第 个查询,路径数分别为 和 ,所以输出 SECOND。
对于第 个查询,改变了检查点 的位置后,再进行第 个查询,路径数分别为 和 ,所以输出 FIRST。
输入示例2
4
1 1
100 100
101 102
199 199
3
2 1 2 2 3
2 1 2 2 4
2 1 2 3 4
输出示例2
FIRST
FIRST
FIRST
请注意,比较的数量可能非常大。
