问题文

高桥君是AtCoder王国的国王。由他统治的AtCoder王国由1到N号城市和相互连接的M条双向道路组成。每条道路都有长度。对于AtCoder王国中任意城市对(A,B)，可以保证从A经过一些道路到达B。

高桥君认为AtCoder国民的幸福程度与交通便利性密切相关。为了调查国民的幸福程度，他想要求出所有可能的城市间最短路径长度的总和S。

假设城市i和j之间的最短路径长度为D(i,j)，则S可以表示为：

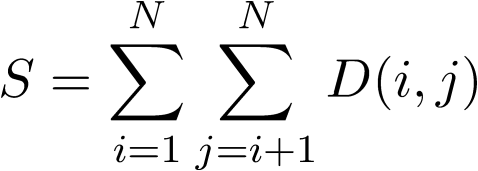
此外，高桥君计划通过公共工程建设K条新的道路。这种情况下，可能会存在两条以上直接连接某些城市对的道路，但已有的道路不会被拆除，而是增加新的道路。

你的任务是编写一个程序，按照给定的顺序逐步建设新道路，并在每次建设后计算上述S的值。

输入

输入以以下格式从标准输入中给出。

N M A1 B1 C1 A2 B2 C2 : AM BM CM K X1 Y1 Z1 : XK YK ZK

• 第一行包含两个整数N（1 ≤ N ≤ 400）和M（1 ≤ M ≤ 1000），分别表示城市数量和道路数量。
• 接下来的M行给出已有道路的信息。其中第i（1 ≤ i ≤ M）行包含三个整数Ai（1 ≤ Ai ≤ N）、Bi（1 ≤ Bi ≤ N）和Ci（1 ≤ Ci ≤ 1000），表示第i条道路连接城市Ai和Bi，并且长度为Ci。确保Ai≠Bi，直接连接同一对城市的道路最多只有1条。
• 可以保证对于AtCoder王国中的任意城市对（A，B），可以通过一些道路从A到达B。
• 第2+M行包含一个整数K（1 ≤ K ≤ 400），表示新建道路的数量。
• 接下来的K行给出新建道路的信息。其中第i（1 ≤ i ≤ K）行包含三个整数Xi（1 ≤ Xi ≤ N）、Yi（1 ≤ Yi ≤ N）和Zi（1 ≤ Zi ≤ 1000），表示第i条新建道路连接城市Xi和Yi，并且长度为Zi。确保Xi≠Yi。

输出

输出以以下格式打印到标准输出中。

第i（1 ≤ i ≤ K）行输出在第i条新建道路后，所有可能的城市间最短路径长度的总和S。

注意：末尾需要换行。

输入示例1

4 3
1 2 1
2 3 1
3 4 10
2
3 4 1
1 4 1

输出示例1

10
8

初始状态如下所示。

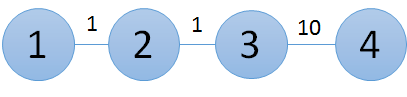
在第一次建设之后，图形变为以下样子。

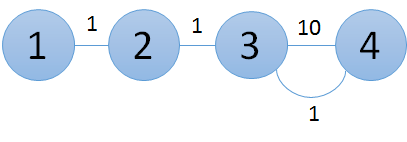
在第二次建设之后，图形变为以下样子。

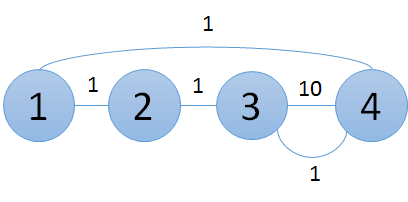
输入示例2

8 16
8 7 38
2 8 142
5 2 722
8 6 779
4 6 820
1 3 316
1 7 417
8 3 41
1 4 801
3 2 126
4 2 71
8 4 738
4 3 336
7 5 717
5 6 316
2 1 501
10
6 1 950
6 1 493
1 6 308
3 4 298
2 5 518
1 5 402
4 7 625
7 6 124
3 8 166
2 4 708

输出示例2

13649
12878
11954
11954
11280
11058
11058
8099
8099
8099